Non Euclidian Geometry(Bolyai)

Bolyai's Appendix(this is an ongoing chapter)

Bolyai Janos(1802-1860)　is one of three founders of non euclidian geometry．

Born in Klausenburg in Transylvania（currently in Rumania，historically in Hungary before occupied by Austria）．Spent young days in Maros-Vaserhely in the same region.
Father, Bolyai Farkas,studied mathematics in Gettingen when Gauss was also there．They often talked about math especially Euclid's parallel postulate.
Discovered non Euclidian Geometry around 23 years old. Have it published in 1831 as an Appendix of his father's math book ,Tentamen．Sent it to Gauss.
Gauss appreciated the paper very much within his circle but did not say anything about the paper in public.
Without any recognition from the public, he became ill. Retired from the Austrian army　and started living on pension in 1933.
He had three children with a common-law wife Rosalie. Their status of not formally getting married and the different idea about math lead Bolyai away from his father. His father died in 1856. Around the same time, he got also apart from Tosalie.
Died at 58 years ols in 1860. The body was buried in a public cemetery near a church. A record of the church said "he died in vain".

Almost all info above , I got from 'Janos Bolyai' by Jeremy J. GRAY(2004) except the last quote which I took from a book "isetu sugakusha retuden" by mori tuyoshi(japanese mathematician). Galoia is very famous for his tragic death(life), but Bolyai can almost match him. （He should have lost this match though.)

His first book is 'Appendix' in 1831 in Latin, later he translate it into German. That book is RaumLehre, which is almost same as Appendix until section 31, but cut short from chapter 32. I read RaumLehre in Japanese translation by prof. Terasaka. He translate RaumLehre until section 31 and translate Appendix from chapter 32.

When I was facinated by non euclidian geometry a few years ago, I started from models(upper sphere model & H+ model) . It was fun because I could enjoy strange geometry and programing also. But after reading Bolyai, I was really impressed by his strong ideas and geographical images. He is like a wizard. He draws unbeliebale lines or even surfaces in the middle of nowhere to me. To probe a theory in a plane(2D) , he sometimes draw a surface and do it in 3D. Before reading his, I had read Lobachevsky and he also use 3D for 2D proof, but his style is too elegant to understand for me. While Bolyai's style seemingly is more of an amature and might lack solid proof sometime, but anyway I love his intuitive way of proof. In addition to that, I am interested in his life too. He was a very passionate mathmatician not only in math but also violin and fencing. One day he is said to win a dozen of opponents drinking wodka! Some day I would like to visit Transylvania. Anyway these are the reasons why I started this page.

Please refer to 'Appendix' to read the proves. There is an English translation. You can find it in such as

'Janos Bolyai' by Jeremy J. GRAY(2004) , 'Non Euclidian Geometry' by BONOLA

But not all versions of BONOLA have the translation. Please make sure you buy the right version.

　In this chapter, "AB|||CD" means AB parallel to CD (they have one infinite point. And AB is not necessarily a segment/line. It can be equi distant line or horicircle). "

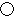AB" means circumferance of a circle centered at A and passes B, while

AB means inside of or square

AB．L means horicircle, F means hori sphere. These names come from Linie（line)& Flache(surface) in German. They are adopted by Bolyai.

Almost all files are written by Geogegra 3.2 & Cabri3D. To manupulate Geogebra files embedded in htmls , you need Java environment (JDK/JRE). You can download JRE from here. To manupulate Cabri3D files, you need plugins for Cabri3D, even if you have Cabri. To download the plugin, check these: cabri2 , cabri3D ． To change the viewpoint in Cabri3D files, drag a mouse with the right buttom down.

At the bottom, there are also original Geogebra&Cabri3D files which you can directly manipulate with Geogebra/Cabri3D SOFTWARE (not plugins)．

If you can read Japanese , you can read detailed explanations of these files and mathematical proves from here. They are PDF files with one to one links to Cabri/Geogebra files.

When you read PDF files and want to return from a link, please use the return key of the browser!! If you use the close button, browser will close.

PDF files (Japanese explanation & links to Geogebra/Cabri3D files)
-please use returen key ,when you return!-
- summary of horicircle &horisphere
- section 22,23,24 (horicircle)
- section 25 (trigonometric function and circumference）
- section 27 (ratio of segment& equi-distant line)
- section 28 (horicircle and angles)
- section 34 (construction of parallel line)
- Personal study
  - Creating H+model from section24&28

Non Euclidian Geometry

mixedmoss.com