![]() 連分数は無理数を分数で近似するときにとても有効です.すなわち分母の小さい項で近似することが出来ます.しかもこれには色々な表示があります.ここでは 通常の入れ子分数表示,長方形表示,フォードの円を簡単に紹介します.紹介は不要という方は下のリンクからすぐアプリをダウンロード,あるいはサイトからご覧下さい.Mathematica
と GeoGebra で作りました.どちらも無料で見ることが出来ます.詳しい説明はWeBでは「数学展望(糸 健太郎)」が,書籍では ブルーバックスの「数論入門」などがあります.ただ後者の方は図形的な表示はありません.一般的な整数論入門となっていて,沢山のトピックを取り上げています.
連分数は無理数を分数で近似するときにとても有効です.すなわち分母の小さい項で近似することが出来ます.しかもこれには色々な表示があります.ここでは 通常の入れ子分数表示,長方形表示,フォードの円を簡単に紹介します.紹介は不要という方は下のリンクからすぐアプリをダウンロード,あるいはサイトからご覧下さい.Mathematica
と GeoGebra で作りました.どちらも無料で見ることが出来ます.詳しい説明はWeBでは「数学展望(糸 健太郎)」が,書籍では ブルーバックスの「数論入門」などがあります.ただ後者の方は図形的な表示はありません.一般的な整数論入門となっていて,沢山のトピックを取り上げています.
![]() 例えば 有理数 a=12/7 の連分数はテキスト表示では [1,1,2,2] です.「入れ子分数表示」と「長方形表示」は,次の様になります.GeoGebraのワークシートのスクリーンショットから取りました.(以下の図は全てスクリーンショット.)
連分数に直すには ユークリッドの互除法と同様に,割る数と割られる数を交互に変えながら,次々に割って作ります.ユークリッドの互除法はこちらをご覧下さい.
例えば 有理数 a=12/7 の連分数はテキスト表示では [1,1,2,2] です.「入れ子分数表示」と「長方形表示」は,次の様になります.GeoGebraのワークシートのスクリーンショットから取りました.(以下の図は全てスクリーンショット.)
連分数に直すには ユークリッドの互除法と同様に,割る数と割られる数を交互に変えながら,次々に割って作ります.ユークリッドの互除法はこちらをご覧下さい.
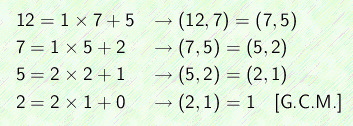 (互除法) (互除法) |
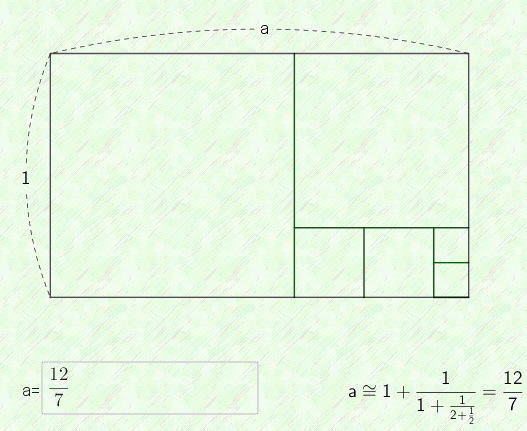 |
![]()
![]() =[1,2,2,2,2,...](2がずーと続く)です.一般に2次の無理数(整数係数の2次方程式の解)の連分数は循環します.
=[1,2,2,2,2,...](2がずーと続く)です.一般に2次の無理数(整数係数の2次方程式の解)の連分数は循環します.

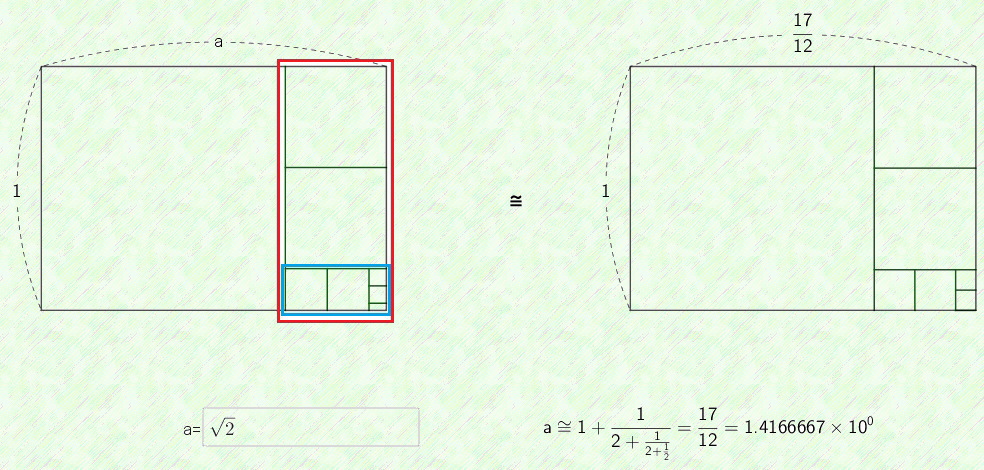
第1〜第3項までの「入れ子分数表示」と「長方形表示」は次の様になります.第3項17/12=1.4166667...でもかなり![]() に近いです.入れ子分数表示では「繰り返し」ですが,長方形表示では「自己相似」となります.即ち,一番下の左の長方形で,赤色と青色の長方形は相似です.これを見たいがために
(Mathematicaで既に作ってあったにも関わらず) GeoGebra でも作成しました.GeoGebra
では 拡大縮小が容易にできるので「マトルーシュカ人形」を目で見ることが出来ます.
に近いです.入れ子分数表示では「繰り返し」ですが,長方形表示では「自己相似」となります.即ち,一番下の左の長方形で,赤色と青色の長方形は相似です.これを見たいがために
(Mathematicaで既に作ってあったにも関わらず) GeoGebra でも作成しました.GeoGebra
では 拡大縮小が容易にできるので「マトルーシュカ人形」を目で見ることが出来ます.
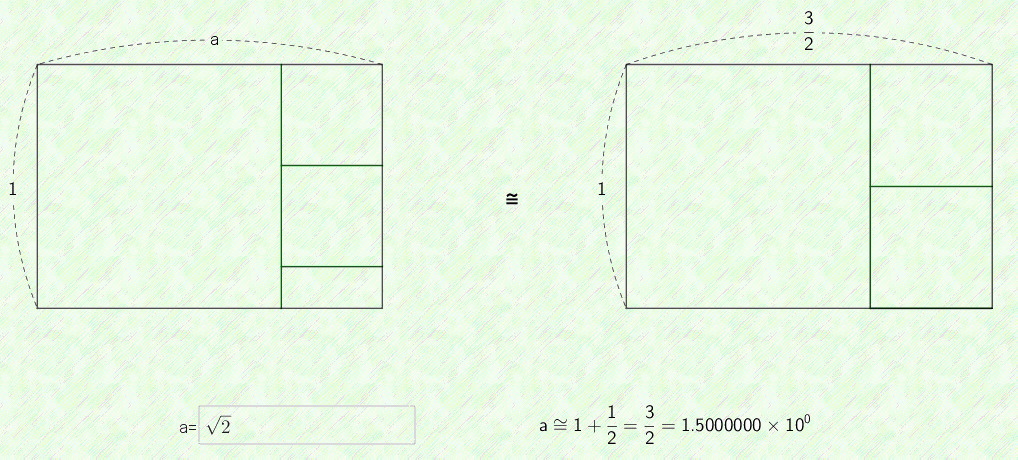 |
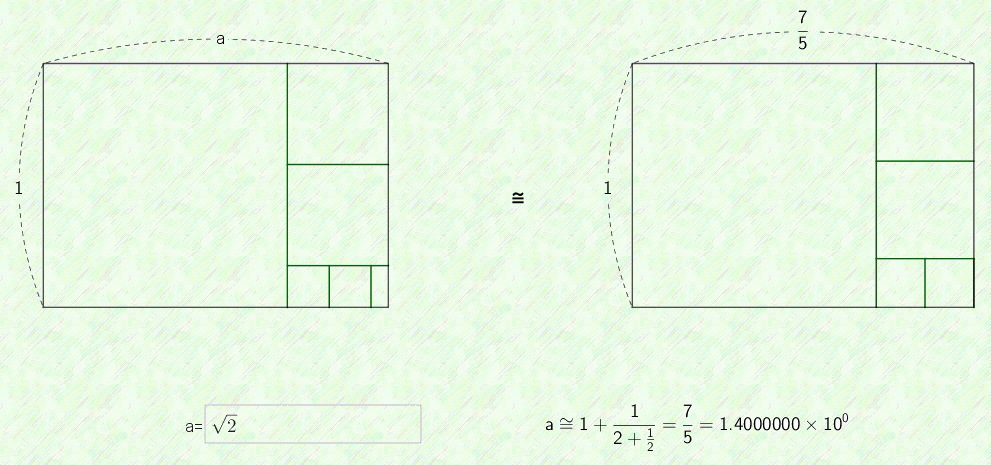 |
 |
![]() 有理数 p/q (p,q は互いに素な自然数) に関するフォードの円 C(p/q) は
有理数 p/q (p,q は互いに素な自然数) に関するフォードの円 C(p/q) は
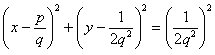 で定義されます.x軸と接し,分母が大きいと急速に半径は小さくなります.例えばC(3/7)とC(1/2)は接点のx座標は1/14しか変わりませんが,
半径は4:49(ほぼ1:12)
です.フォードの円については「数学展望(糸 健太郎)」が非常に詳しくまた分かりやすいです.フォードの円には次の3つの基本性質があります.
で定義されます.x軸と接し,分母が大きいと急速に半径は小さくなります.例えばC(3/7)とC(1/2)は接点のx座標は1/14しか変わりませんが,
半径は4:49(ほぼ1:12)
です.フォードの円については「数学展望(糸 健太郎)」が非常に詳しくまた分かりやすいです.フォードの円には次の3つの基本性質があります.

2つの有理数q/pとs/rが |ps-qr|=1 を満たす時,これらの有理数は「隣り合う」と定義します.そして連分数の近似分数展開に置いて隣接2項は「隣り合い」ます.
例えば![]() の近似分数展開は次の様になりますが,確かに隣接2項は「隣り合って」います.
の近似分数展開は次の様になりますが,確かに隣接2項は「隣り合って」います.
![]() →
→ 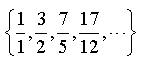 (注: 分母と分子の漸化式を作って証明します. 「数学的帰納法で証明せよ」とかのヒントをつければ,大学入試でも出題できるレベルです.)
(注: 分母と分子の漸化式を作って証明します. 「数学的帰納法で証明せよ」とかのヒントをつければ,大学入試でも出題できるレベルです.)
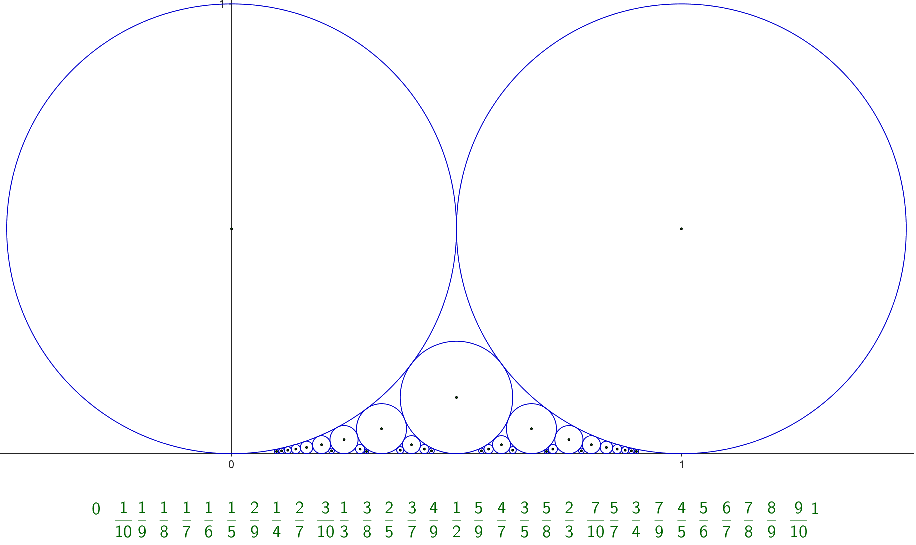
例えば0/1以上1/1以下で分母が10以下の有理数(ファレ‐分数)に対するフォードの円は上図のようになります.分母が10より大きい分数もすべて並べると,上の円とx軸の間にどんどん接しながら入っていきます.
そして,実数aの近似分数に対するフォードの円を順に作っていくと,それらの円は順に接しながら,その接点のx座標が
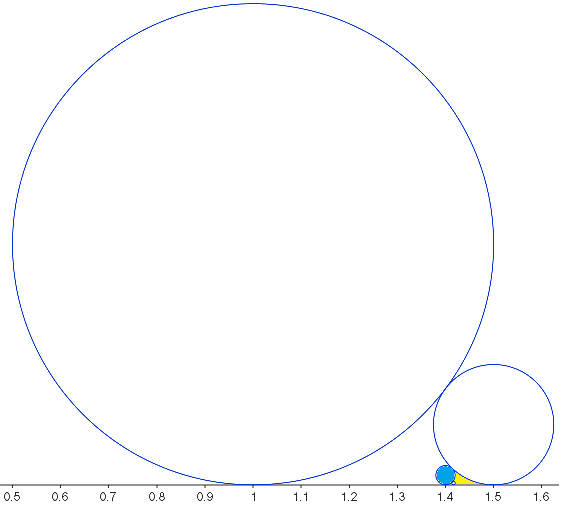
a に近づいていきます.下の図は ![]() の近似分数展開のフォードの円です.4つ目の C(17/12) は小さくて見えづらいですが,GeoGebra の拡大機能を使うと よく見ることが出来ます.これは「マトルーシュカ」人形ではないですが,次々にA (
の近似分数展開のフォードの円です.4つ目の C(17/12) は小さくて見えづらいですが,GeoGebra の拡大機能を使うと よく見ることが出来ます.これは「マトルーシュカ」人形ではないですが,次々にA (![]() ,0) を囲むように(VIPをガードするかの様に)Aに近づいて行きます.基本定理(1)より,フォードの円は交わることがないので,このガードを破って他のフォードの円がAに近づくことは難しいです.これを使うと,最良近似定理とラグランジュの定理が簡単に証明されます.
,0) を囲むように(VIPをガードするかの様に)Aに近づいて行きます.基本定理(1)より,フォードの円は交わることがないので,このガードを破って他のフォードの円がAに近づくことは難しいです.これを使うと,最良近似定理とラグランジュの定理が簡単に証明されます.
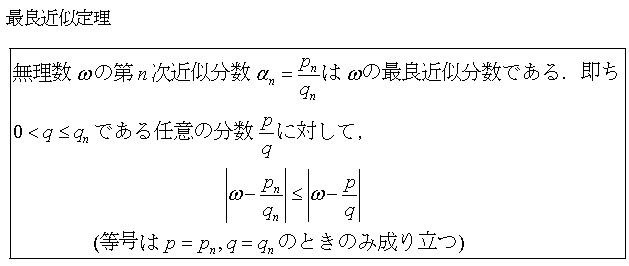 |
 |
![]() 上に上げた「入れ子分数表示」と「長方形表示」と「フォードの円」を「動的に」求めるワークシートを
GeoGebra で作成しました.また「入れ子分数表示」と「長方形表示」を動的に求めるノートブックを
Mathematica で作成しました.
上に上げた「入れ子分数表示」と「長方形表示」と「フォードの円」を「動的に」求めるワークシートを
GeoGebra で作成しました.また「入れ子分数表示」と「長方形表示」を動的に求めるノートブックを
Mathematica で作成しました.
ノートブックは Mathematica 用です.Mathematica のサイトで見ることも出来ますが,やはりやや重いです.やはりダウンロードして MathematicaかWolfram plyerで見る方が軽いです.「Wolfram player」 は無料でダウンロード&インストールすれば,分数表示と長方形表示を「動的に」 (interactiveに) 求める事ができます.しかし Mathematica をお持ちの方とは異なり,コマンドラインは利用できません.2023年8月現在で「wolfram player」 は Windows,Mac,Linux そして iOS 用があります.(Android用はまだありません.) Wolframによるやや詳しい説明(ダウンロードなど)もここ(Windows)とここ(Mac)にあります.
| 1.GeoGebra のサイト | 連分数の長方形表示 |
| 連分数とフォードの円 | |
| フォードの円とファレ‐数列 | |
| ユークリッドの互除法 | |
| 2.Mathematica のサイト | 連分数の長方形表示と入れ子分数表示 |
| 3.ggb file Download | 連分数&フォードの円全て(zipped) |
| 4.notebook(コマンドライン含む) Download | 連分数の長方形表示と入れ子分数表示 |
| notebook(モバイル版) Download | 同上(mobile用) |
| GeoGebra Download | GeoGebra Download |
| Wolfram Player download | wolfram player |
| by 生越 茂樹(Ogose Shigeki). | All rights reserved. |