で定まる漸化式は y=f(x)とy=xのグラフを利用して，目で見ることが出来ます．以前　 Mathematica を使って作ったのですが，より多くの人が利用できるように，GeoGebra でも作ってみました．ただしGeoGebraでは再起による関数定義はできないので，余り複雑なことは出来ません．(a_n+1=f(a_n)という定義はできません.) でも無料でかつ画面も大きくて,拡大縮小が容易です．

• デフォルトでは f(x)=a x(1-x) というカオス理論で有名な関数（ロジステック写像）ですが，関数は自由に変えられます．下の例では初めの3つはロジステック写像で　最後は半円です．
• 関数を変えるのは TextField に入力します．例えば，f(x)=sqrt(4x-x^2)と入力すると， となります．
• ロジスティック関数の場合，a　の値により {a_n}の極限は次の様に変化します．（「カオスとフラクタル」山口昌也著より)
  • 0<a<1のときは 0に収束
  • 1≦a≦2のとき 1-1/a に単調に収束
  • 2<a≦3の時 1-1/a に振動収束
  • 3<a≦1+√6(≒3.45) のとき　周期2の振動(偶数項と奇数項で別々の値に収束).
  • 1+√6<a<c(≒3.57)のとき 4,8,16...周期の振動がaの値が増えるごとに出現．
  • c<aのときカオス．（あらゆる周期の軌道．さらに周期を持たない軌道が現れ，a₁の値に極めて敏感に反応する)

以下の3つはロジスティック写像 [1-1] a=2.5の時
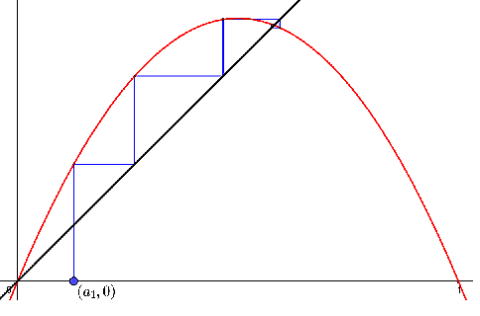[1-2] a=3.2の時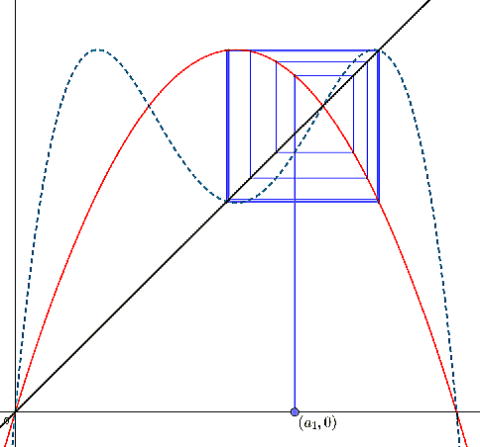
[1-3] a=3.9の時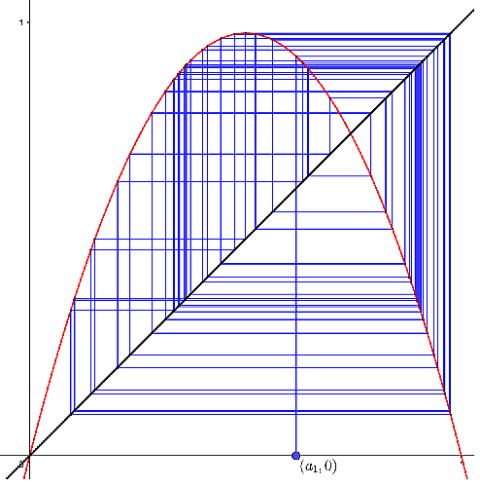
[2-1] の時

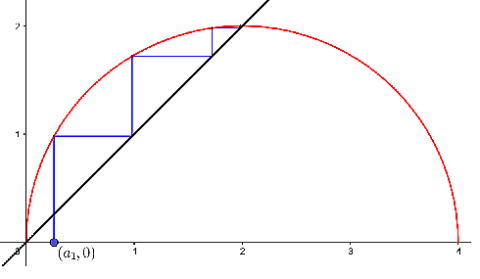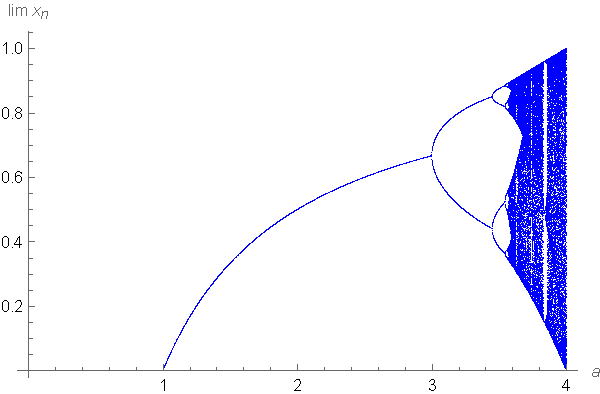
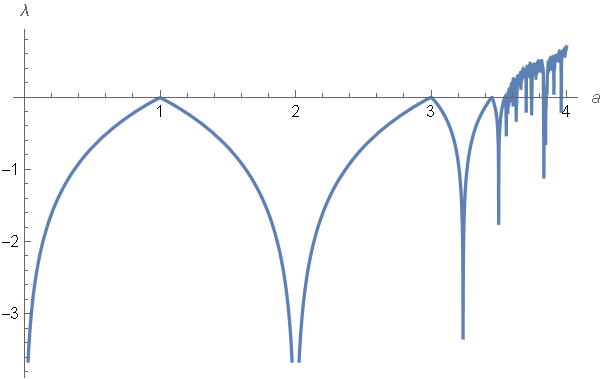
ロジクテイック写像 y=a x(1-x) で aの値を横軸，lim x_n を縦軸に取ったグラフ（分岐ダイヤグラム)とリアプノフ指数λです． こちらはGeoGebraでは作れませんでした． Mathematica か Wolfram Player（無料) でないと見れません．

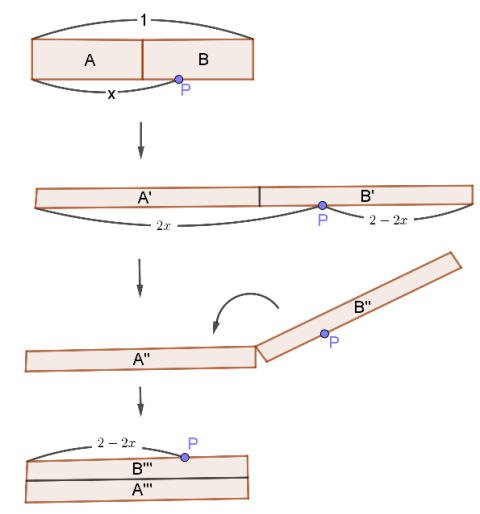
パイコネ変換．先ず，小麦粉と水を混ぜて長さ１のベースを作ります．これに対し操作Aを「半分の厚さに成るまで押しつぶし，真ん中で切って重ね，元の厚さに戻す」とし，Aを何回も繰り返します．この時，左端の点を原点，底辺上の任意の点をP(x)とし，一回の操作後のPのx座標をｆ（ｘ）とおくと f(x) は次の式となります．（0<x<1/2の時は明らか．1/2<x<1の時は，下図から）

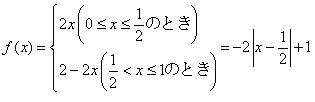
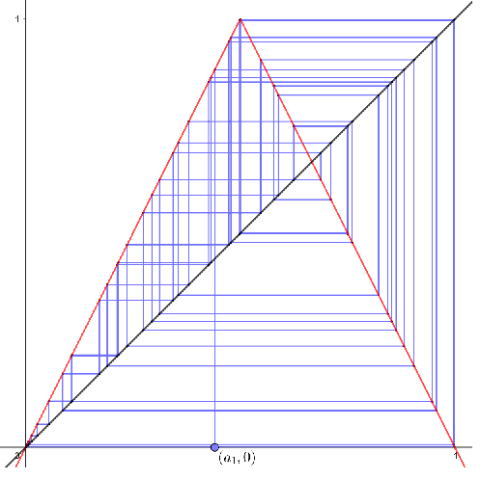
このパイコネ変換では{a_n}はカオスではありますが，より強い「ランダム」になっています．（ロジステイックでもa=4とすればランダムとなります). 即ち「0<f(x)<1/2→A, 1/2<f(x)<1→B」 を対応させると，初期値を変えることによって任意のA,Bの数列を作ることが出来ます．A,Bをそれぞれコインの表と裏とすると，任意の長さのコイン投げと同じ数列が，初期値を変えるだけで作れるということです．これをGeoGebra で入力するには TextFieldで 「f(x)=-2 abs(x-0.5)+1」 とします．

GeoGebraのファイルは，GeoGebra の公開サイトで見ることが出来ます．ダウンロードも可能ですが 見るにはGeoGebra（無料） が必要です．ちなみに私は「クラシック ５」を愛用していて，これも「クラッシック5」で作成しました．(因みにクラシック ６はWeB用でやたら操作ボタンとか大きすぎる気がして好きでありません．また幾何とか数式処理とかに特化したバージョンは，Mobile用だと個人的には思います．しかし「幾何ヴァージョン」でも「クラシック ６」でも動くはずです．)　

同様のグラフと漸近線をMathematica の notebookでも見れます．notebook では 分岐ダイヤグラムも見ることが出来ます．notebook を見るには，Mathematica 或いは　Wolfram Player が必要です．Wolfram Player は 2023年8月現在で，Windows, Mac, Linux, iOS 用があります．Android用はまだです．Wolfram Player は 無料ですが，数字以外の入力は出来ません．從って　デフォルトの関数以外にはセット出来ません．その場合は GeoGebra の方をご利用ください．

Contents

1.GeoGebra のサイトで	At Geogebra site
2.gb file Download	Recurrence.gb
3.Notebook Download	Chaos.nb
GeoGebra Download	GeoGebra.org
Wolfram Player Download	Player download

トップページへ戻る	Email me
by 生越　茂樹(Ogose Shigeki).	All rights reserved.