other_surfaces

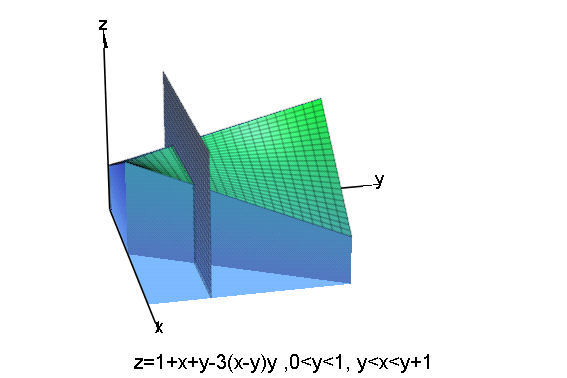
[1]. z=1+x+y-3(x-y)y ,0<y<1, y<x<y+1 の表す領域
曲面は plot::Surface を使ってかきますが，「変域は x=0..1 のように定数でないといけない」ので
領域によっていろいろ工夫が必要になります．この場合は次のようにして簡単に描くことができます．
与式は「z=1+(x-y)+2y-3(x-y)y (0<y<1, 0<x-y<1)」と同値．よって t=x-y とおくと x=y+t だから
(x,y,1+(x-y)+2y-3(x-y)y) (0<y<1, 0<x-y<1) <-> (y+t, y,1+t+2y-3ty) (0<y<1, 0<t<1)
ゆえに，(x,y,z)=(x,y,1+x+y-3(x-y)y) ,0<y<1, y<x<y+1 という曲面は次のようになります．

surface1:=plot::Surface([t+y,y,1+t+2*y-3*t*y],y=0..1,t=0..1,Color=RGB::Green):

これに側面を付け加えます．例えば平面x=y による surface1 の切り口は「(x,y,z)=(x,x,z), 0<x<1, 0<z<1+2x」ですが変域は定数でないといけないので相似パラメータを使って，「(x,y,z)=(x,x,(1+2x)v),0<x<1,0<v<1」のようにします．同様に他の側面も作って 1つにまとめます．

body1:=plot::Group3d(
   surface1,
   plot::Surface([x,x,(1+2*x)*v],x=0..1,v=0..1,ULinesVisible=FALSE,VLinesVisible=FALSE
,Color=RGB::Aqua),//x=yによる立体の切り口
   plot::Surface([x,x-1,v*(3-x)],x=1..2,v=0..1,ULinesVisible=FALSE,VLinesVisible=FALSE
,Color=RGB::Aqua),//x=y+1による立体の切り口
   plot::Surface([x,0,(1+x)*v],x=0..1,v=0..1,ULinesVisible=FALSE,VLinesVisible=FALSE
,Color=RGB::DarkBlue),//y=0による立体の切り口
   plot::Surface([x,1,(-2*x+5)*v],x=1..2,v=0..1,ULinesVisible=FALSE,VLinesVisible=FALSE
,Color=RGB::DarkBlue),//y=1による立体の切り口
   plot::Surface([u,v,0],u=0..2,v=0..1,Color=RGB::Grey,
ULinesVisible=FALSE,VLinesVisible=FALSE)//xy平面
):

これに断面「y=k」を付け加えます．k がアニメーションパラメーターになります．

section1:=plot::Surface([u,k,v],u=0..2,v=0..3,k=0..1,Color=RGB::Grey40):

myAxes:=plot::Group3d(
plot::Arrow3d([0,0,0],[2.5,0,0],Color=RGB::Black),plot::Text3d("x",[2.5,0,0])
,plot::Arrow3d([0,0,0],[0,1.5,0],Color=RGB::Black),plot::Text3d("y",[0,1.5,0])
,plot::Arrow3d([0,0,0],[0,0,4],Color=RGB::Black),plot::Text3d("z",[0,0,4])):

plot(body1,section1,Axes=None,myAxes,Footer="z=1+x+y-3(x-y)y ,0<y<1, y<x<y+1")

一般の曲面で「(x,y,f(x,y)), a<x<b, 0<y<g(x) 」という場合も「(x, t*g(x), f(x,t*g(x)), a<x<b, 0<t<1」とすれば，曲面を描くことができます．

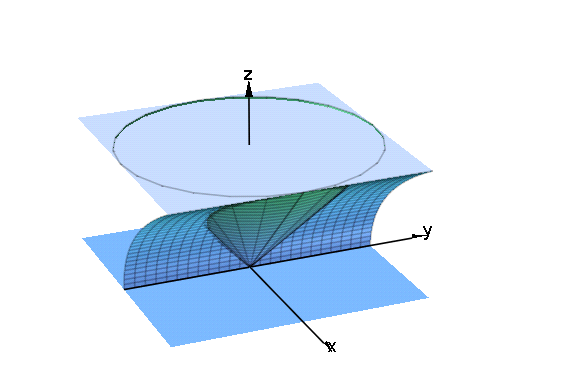
[2]. x²+y²<z², z²<x, 0<z<1 で表される領域を描きます．まず単純に円すい「x²+y²<z^2」と放物面「z²<x」，平面「z=0」,　「z=1」の4つの曲面を描くことにします．
plot::ZRotate(f(x),x=a..b) は z=f(x)をz軸の周りに回転した曲面を描きます．これを使って円錐を描きます．

mycone:=plot::ZRotate(x,x=0..1,Color=RGB::ForestGreen):

plot::Surface を使って　放物面と平面を描きます．

myparabola:=plot::Surface([u^2,v,u],u=0..1,v=-1..1,Color=RGB::Aqua):

myplanes:=plot::Group3d(plot::Surface([u,v,0],u=-1..1,v=-1..1,Color=RGB::Grey
                    ,ULinesVisible=FALSE,VLinesVisible=FALSE),
                   plot::Surface([u,v,1],u=-1..1,v=-1..1,
                   ULinesVisible=FALSE,VLinesVisible=FALSE,Color=RGB::Grey)):

myAxes:=plot::Group3d(plot::Arrow3d([-1.5,0,0],[1.5,0,0],Color=RGB::Black),
plot::Arrow3d([0,-1.0,0],[0,1.5,0],Color=RGB::Black),
plot::Arrow3d([0,0,0],[0,0,1.5],Color=RGB::Black),
plot::Text3d("x",[1.5,0,0]),plot::Text3d("y",[0,1.5,0]),plot::Text3d("z",[0,0,1.5])):

plot(mycone,myparabola,myplanes,myAxes,Axes=None)

今度は放物面と円すいで囲まれる立体だけを表示してみます．そのために [x²+y²=z² ，x=z²]から z を消去すると x²+y²-x=0 これは中心が(1/2,0,0)で半径が1/2の円を表すので，この円の内部の領域は「(x,y)=(v(1+cos(t)), v sin(t)) v=0..1/2, t=0..2*PI」と表されます． (v は半径とは違います.　単なるパラメータです.) このように変域が定数の変数 v,t を使って x,y　が表されれば　後は簡単です．放物面の式に代入して　「z=sqrt(x)=sqrt(v(1+cos(t))=sqrt(2v)cos(t/2)」. 円錐面の式に代入して　「z=sqrt(x²+y²)=v*sqrt((1+cos(t))²+sin²(t))=2v cos(t/2)」よって，次のようにすれば　放物面と円すいで囲まれる立体だけが表示されます．

mycone2:=plot::Surface([v*(1+cos(t)),v*sin(t),2*v*abs(cos(t/2))],
                 v=0..1/2,t=0..2*PI,Color=RGB::ForestGreen):
myparabola2:=plot::Surface([v*(1+cos(t)),v*sin(t),abs(cos(t/2))*sqrt(2*v)],
        v=0..1/2,t=0..2*PI,Color=RGB::Aqua):
camera := plot::Camera([2*cos(-a-PI/4), 2*sin(-a-PI/4), 1.2],
                       [0, 0, 0], PI/3, a = 0..2*PI,
                       Frames = 100):
plot(mycone2,myparabola2,myAxes,Axes=None,camera)

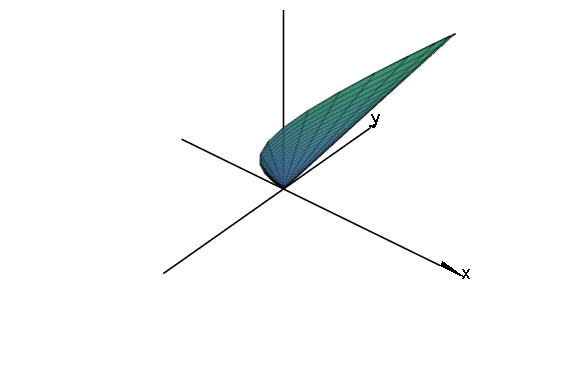
[3]. x+y+z<3, x+2z<4, y-z<1, x>0, y>0, z>0 の表す領域
6個の平面によって囲まれる立体なので　多角形を描く plot::Polygon3d を使います．これは任意の数の点をつなげて多角形を描くことができますが，「内部の塗りつぶし」は三角形に限ります．(同一平面上に有ってもだめです.) よって plot::Polygon3d　では三角形を何個かつなげて4角形や，5角形を描かないといけません．これは5角形の時には3個も三角形を書くことになり　やや面倒なので，同一平面上にある任意の凸多角形を塗りつぶせるようにプログラムします．

myPolygon3d:=proc(points,color)
      local n,base,mypoly;
      begin
         n:=nops(points): //points の要素の数が n
         base:=op(points,1)://base は points の最初の要素
         mypoly:=plot::Polygon3d([base,op(points,k),op(points,k+1)],
             FillColor=color,Closed=TRUE,LinesVisible=FALSE,Filled=TRUE)$k=2..n-1:
             //1番目の点,k番目の点,(k+1)番目の点をつなげて plot::Polygon3d を n-2個作る
      return(mypoly):
end_proc;

このプログラムを使って平面を6個作ります．

poly1:=myPolygon3d([[3,0,0],[2,1,0],[0,2,1],[0,1,2],[2,0,1]],RGB::SeaGreen):
poly2:=myPolygon3d([[3,0,0],[2,0,1],[0,0,2],[0,0,0]],RGB::Violet):
poly3:=myPolygon3d([[2,0,1],[0,1,2],[0,0,2]],RGB::LightYellow):
poly4:=myPolygon3d([[0,0,2],[0,1,2],[0,2,1],[0,1,0],[0,0,0]],RGB::Blue):
poly5:=myPolygon3d([[0,0,0],[3,0,0],[2,1,0],[0,1,0]],RGB::Aqua):
poly6:=myPolygon3d([[2,1,0],[0,1,0],[0,2,1]],RGB::DarkBlue):

myAxes:=plot::Group3d(
plot::Arrow3d([-0,0,0],[3.5,0,0],Color=RGB::Black),plot::Text3d("x",[3.5,0,0])
,plot::Arrow3d([0,0,0],[0,2.5,0],Color=RGB::Black),plot::Text3d("y",[0,2.5,0])
,plot::Arrow3d([0,0,0],[0,0,2.5],Color=RGB::Black),plot::Text3d("z",[0,0,2.5])
):

plot(poly1,poly2,poly3,poly4,poly5,poly6,myAxes,Axes=None,
Footer=" x+y+z<3, x+2z<4, y-z<1, x>0, y>0, z>0")

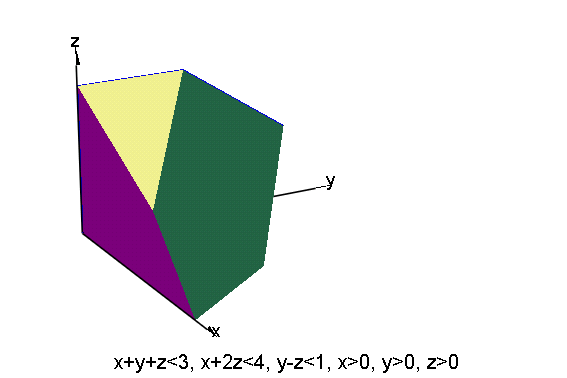
この立体を平面z=tで切った断面を描きます．断面は 0<t<1 のときは 4点 (0,0,t), (3-t,0,t), (2-2t,t+1,t), (0,t+1,t) で囲まれる四角形 section1, 1<t<2 のときは 4点 (0,0,t), (4-2t,0,t), (4-2t,t-1,t), (0,3-t,t) で囲まれる四角形 section2 となります．アニメーションにしたいので，先に作った myPolygon3d に TimeRange を付け加えます．さらに今度は　断面をはっきり見せるために多角形の「外周」も付け加えます．「外周」は　plot::Polygon3d でも任意の点をつなげて作ることができますが，辺によって色を変えたいのでLine3dを使ってみます． (plot::Polygon3d でも LineColorFunction を定義すれば線分によって色を代えることもできます.) fillcolor は面の色，linecolors は辺の色です .

myPolygon:=proc(points,fillcolor,linecolors,time)
      local n,base,polybody,polyframe;
      begin
         n:=nops(points):
         base:=op(points,1):
         polybody:=plot::Polygon3d([base,op(points,k),op(points,k+1)],
             FillColor=fillcolor,Closed=TRUE,LinesVisible=FALSE,Filled=TRUE)$k=2..n-1:
         polyframe:=plot::Line3d(op(points,k),op(points,k+1),
                   Color=op(linecolors,k))$k=1..n-1
                   ,plot::Line3d(op(points,1),op(points,n),Color=op(linecolors,n)):
         return(plot::Group3d(polybody,polyframe,TimeRange=time)):
end_proc:

linecolors1:=[RGB::DarkBlue,RGB::Green,RGB::Violet,RGB::Aqua]:

linecolors2:=[RGB::DarkBlue,RGB::Yellow,RGB::Green,RGB::Aqua]:

0..5秒は section1 が , 5..10秒は section2 が見えるアニメーションです．

section1:=myPolygon([[0,0,t/40],[3-t/40,0,t/40],[2-2*t/40,t/40+1,t/40],[0,t/40+1,t/40]],
RGB::Blue,linecolors1,t/8..5)$t=0..40:

section2:=myPolygon([[0,0,t/40],[4-2*t/40,0,t/40],[4-2*t/40,t/40-1,t/40],[0,3-t/40,t/40]],
RGB::Blue,linecolors2,t/8..10)$t=40..80:

plot(section1,section2,VisibleBeforeBegin=FALSE)

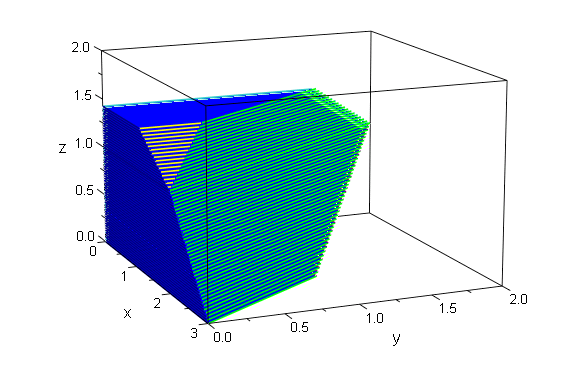
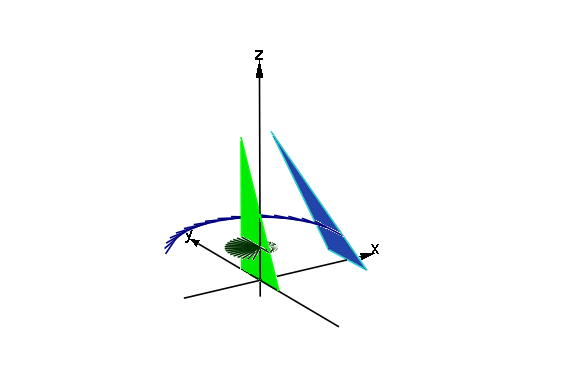
[4]. xyz空間で P(t,sin(t),0), Q(t, t+1,0) とし，線分PQの真上に点Rを三角形PQRが正三角形になるように取ります．
0<t<pi のとき三角形PQRの通過する領域を描きます．まず P,Q,R の座標を関数にします．

P:=t->[t,sin(t),0]: Q:=t->[t,t+1,0]: R:=t->[t,(t+1+sin(t))/2,sqrt(3)/2*(t+1-sin(t))]:

これを使って三角形PQRを作って　plot します．(t が入っているので　アニメーションになります.)

triangle:=plot::Polygon3d([P(t),Q(t),R(t)],
Filled=TRUE,Closed=TRUE,t=0..PI):

curve1:=plot::Curve3d([t,sin(t),0],t=0..PI):
curve2:=plot::Curve3d([t,t+1,0],t=0..PI):
names:=plot::Group3d(
                    plot::Text3d("P",P(t),t=0..PI),
                    plot::Text3d("Q",Q(t),t=0..PI),
                    plot::Text3d("R",R(t),t=0..PI)
       ):

plot(triangle,names,curve1,curve2)

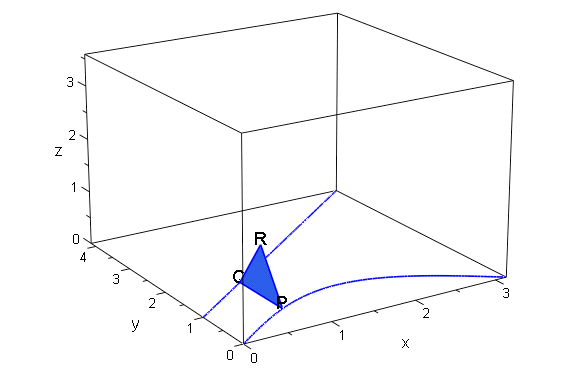
これではよく分からないので，三角形をつなげて描きます．TimeRange を設定して，「VisibleBeforeBegin=FALSE」と共に plot すれば次々に三角形が加わっていくアニメーションになります．

body:=plot::Polygon3d([P(PI/20*t),Q(PI/20*t),R(PI/20*t)],Closed=TRUE
,TimeRange=t/2..(t+1)/2)$t=0..20:
plot(body,names,curve1,curve2,VisibleBeforeBegin=FALSE)

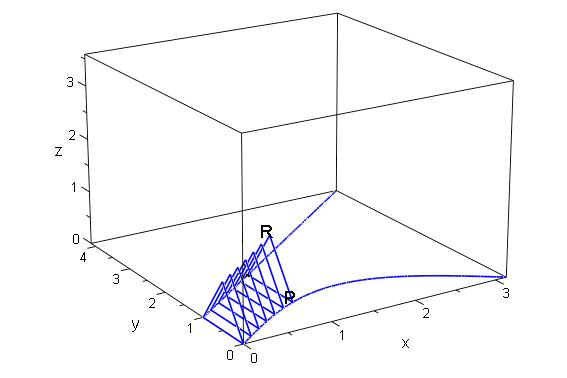
さらに　三角形PQRの通過する曲面を描きます．そのためにまず Pの y 成分を対応させる関数 Py を作ります．これは Py:=t->sin(t) としても良いですが，先に P:=t->[t,sin(t),0] としたので Py:= t-> op(P(t),2) で作ります．

Py:=t->op(P(t),2):

同様にして Pのz成分を対応させる関数 Pz, Qのy成分を対応させる関数Qyなども作ります．

Pz:=t->op(P(t),3):
Qy:=t->op(Q(t),2): Qz:=t->op(Q(t),3):
Ry:=t->op(R(t),2): Rz:=t->op(R(t),3):

これを使って　「線分PQの描く　surface1 」，「QRの描く　surface2」, 「PRの描く　surface3」　を作ります．

surface1:=plot::Surface([t,(1-s)*Py(t)+s*Qy(t),(1-s)*Pz(t)+s*Qz(t) ],
          t=0..PI,s=0..1,FillColor=RGB::Green):
surface2:=plot::Surface([t,(1-s)*Ry(t)+s*Qy(t),(1-s)*Rz(t)+s*Qz(t) ],
          t=0..PI,s=0..1,FillColor=RGB::Aqua):
surface3:=plot::Surface([t,(1-s)*Py(t)+s*Ry(t),(1-s)*Pz(t)+s*Rz(t) ],
          t=0..PI,s=0..1,FillColor=RGB::Violet):

plot(surface1,surface2,surface3)

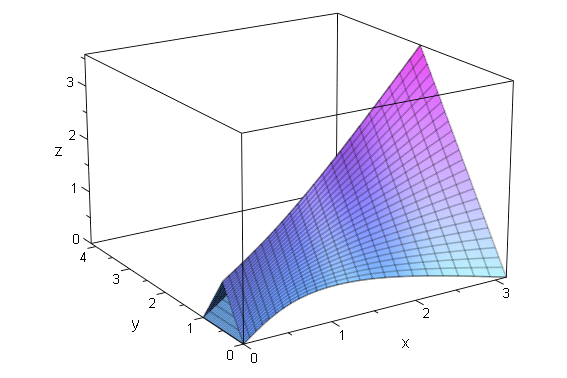
さらにもう一個パラメータaを増やすと，今度は surface1, surface2, surface3 の「アニメーション」になります．

animatedsf1:=plot::Surface([t,(1-s)*Py(t)+s*Qy(t),(1-s)*Pz(t)+s*Qz(t)],
             t=0..a*PI,s=0..1,a=0..1,Color=RGB::Green):
animatedsf2:=plot::Surface([t,(1-s)*Ry(t)+s*Qy(t),(1-s)*Rz(t)+s*Qz(t) ],
          t=0..a*PI,s=0..1,a=0..1,Color=RGB::Aqua):
animatedsf3:=plot::Surface([t,(1-s)*Py(t)+s*Ry(t),(1-s)*Pz(t)+s*Rz(t) ],
          t=0..a*PI,s=0..1,a=0..1,Color=RGB::Violet):

plot(animatedsf1,animatedsf2,animatedsf3)

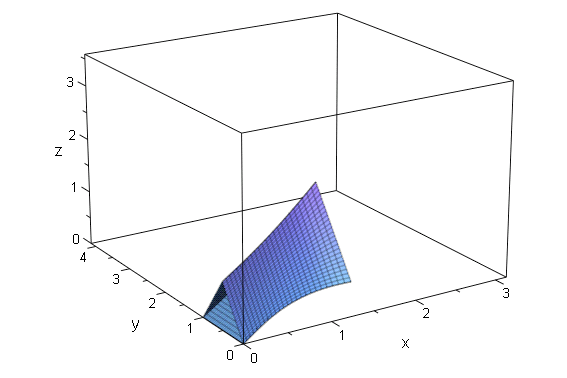
[5]. xy平面上の原点を中心とする半径1の円C上の点Pと，平面z=2上の点A(0,0,2)を中心とし半径1の円D上の点をQとする． Pが円C上を動く時線分PQの描く曲面．　ただし Qの位相(角)は Pの位相より90度大きいとします．まず PとQの座標を関数にします．

P:=t->[cos(t),sin(t),0]: Q:=t-> [cos(t+PI/2),sin(t+PI/2),2]:

次に線分PQを作って　TimeRange も設定し　アニメーションにします．

seg:=plot::Line3d(P(PI/20*t),Q(PI/20*t),TimeRange=t/4..10)$t=0..40:
upperCircle:=plot::Circle3d(1,[0,0,2],Color=RGB::Gray50):
lowerCircle:=plot::Circle3d(1,[0,0,0],Color=RGB::Gray50):

plot(seg,upperCircle,lowerCircle,VisibleBeforeBegin=FALSE)

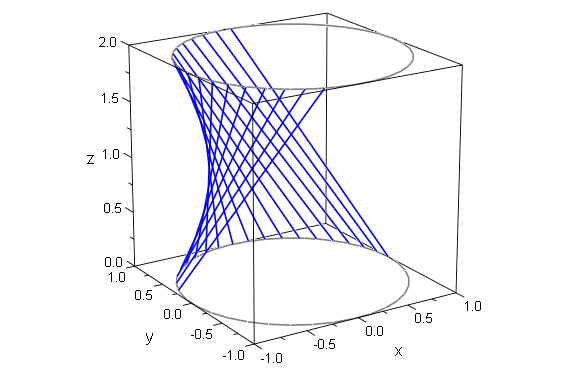
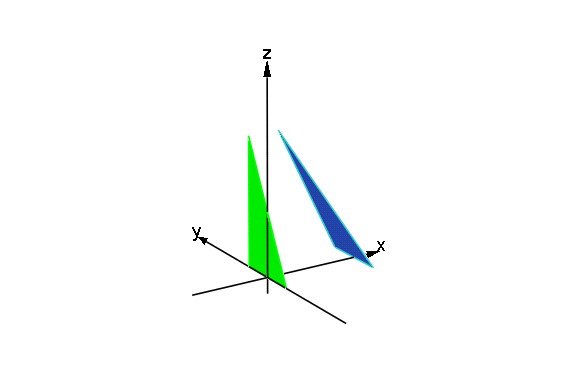
[6]. 空間での平面図形の回転体． A(1,1,4),B(3,-1,0),C(3,1,0)を3点とする三角形ABCと　，そのyz平面への正射影の三角形A'B'C' を回転させる．２つの回転体の体積は等しい． plot::Polygon3d をつかって三角形を2つつくり，それを Rotate3d でアニメーションにする．

tri1:=plot::Polygon3d([[1,1,4],[3,-1,0],[3,1,0]],Color=RGB::Aqua,
Closed=TRUE,Filled=TRUE):
tri2:=plot::Polygon3d([[0,1,4],[0,-1,0],[0,1,0]],Color=RGB::Green,
FillColor=RGB::Green,Closed=TRUE,Filled=TRUE):

myAxes3:=plot::Group3d(
plot::Arrow3d([-2.5,0,0],[4,0,0],Color=RGB::Black),plot::Text3d("x",[4,0,0])
,plot::Arrow3d([0,-4,0],[0,4,0],Color=RGB::Black),plot::Text3d("y",[0,4,0])
,plot::Arrow3d([0,0,-0.5],[0,0,6.5],Color=RGB::Black),plot::Text3d("z",[0,0,6.5])
):

plot(plot::Rotate3d(a,tri1,a=0..2*PI),plot::Rotate3d(a,tri2,a=0..2*PI),myAxes3,Axes=None)

z=k による断面積が等しいので　この二つの回転体の体積は等しい．それが分かるように z=1 による断面の線分を作って回転させた．しかし，Rotate3dでやると　「軌跡が残らない」ので，数列生成子「$」を使ってたくさんの線分を作成し，それらのTimeRangeを変えることにより次々に線分が移っていく様子が見えるようにした．このとき VisibleBeforeBegin=FALSE にして　TimeRange に入る前には見えないように設定する．（default では VisibleBeforeBegin=TRUE になっている.) アニメーションは20秒続くが，19秒から20秒の間に線分を囲む円を作り,線分の軌跡がよく分かるようにした．

z:=1:
seg1:=plot::Line3d(
   [(6-z)/2*cos(t/PI/2)-(z-2)/2*sin(t/PI/2),(6-z)/2*sin(t/PI/2)+(z-2)/2*cos(t/PI/2),z],
   [(6-z)/2*cos(t/PI/2)-sin(t/PI/2),(6-z)/2*sin(t/PI/2)+cos(t/PI/2),z],Color=RGB::DarkBlue
,TimeRange=t/2..20)
$t=0..40:
seg2:=plot::Line3d(
[-(z-2)/2*sin(t/PI/2),(z-2)/2*cos(t/PI/2),z],
   [-sin(t/PI/2),cos(t/PI/2),z],Color=RGB::DarkGreen,TimeRange=t/2..20)
$t=0..40:
circles:=plot::Group3d(
      plot::Circle3d(1,[0,0,1],Color=RGB::DarkGreen),
      plot::Circle3d(2.5,[0,0,1],Color=RGB::DarkBlue),
      plot::Circle3d(sqrt(29)/2,[0,0,1],Color=RGB::DarkBlue)
     ,TimeRange=19..20):

plot(seg1,seg2,circles,tri1,tri2,myAxes3,Axes=None,VisibleBeforeBegin=FALSE)