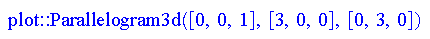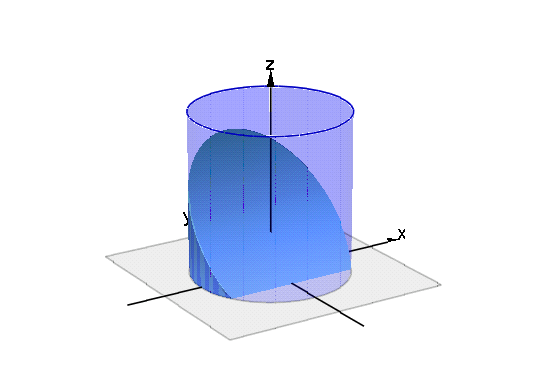
[1 ]. 2本の円柱
「x²+z²=1, x²+y²=1」 の共通部分の曲面を書きます．

「(cos(t),sin(t),0)を通りz軸に平行な直線」と, 「x²+z²=1」との交点を求めると
「P(cos(t),sin(t),sin(t)), Q(cos(t),sin(t),-sin(t))」. よって線分PQの描く曲面は
(x,y,z)=(cos(t),sin(t),s)(0<t<2pi, -sin(t)<s<sin(t)). しかし
変数が[u=-1..1]のように定数でないといけないので，(もっといい方法があるかもしれませんが）私は
相似比をパラメータとして「(x,y,z)=(cos(t),sin(t),sin(t)*v)(0<t<2pi, -1<v<1).」としてます．これで
曲面の半分ができるので，同様にしてあとの半分も作ります．

• cone1:=plot::Surface([cos(u),sin(u),sin(u)*v],u=0..2*PI,v=-1..1,
  ULinesVisible=FALSE,VLinesVisible=FALSE,Color=RGB::Green):

• cone2:=plot::Surface([cos(u),sin(u)*v,sin(u)],u=0..2*PI,v=-1..1,
  ULinesVisible=FALSE,VLinesVisible=FALSE,Color=RGB::Blue):
  

高校の教科書にあわせて x,y,z 軸も作り Group3d でまとめます．

• myAxes:=plot::Group3d(
  plot::Arrow3d([-2,0,0],[2,0,0],Color=RGB::Black),plot::Text3d("x",[2,0,0])
  ,plot::Arrow3d([0,-2,0],[0,2,0],Color=RGB::Black),plot::Text3d("y",[0,2,0])
  ,plot::Arrow3d([0,0,-2],[0,0,2],Color=RGB::Black),plot::Text3d("z",[0,0,2])):  
  
  

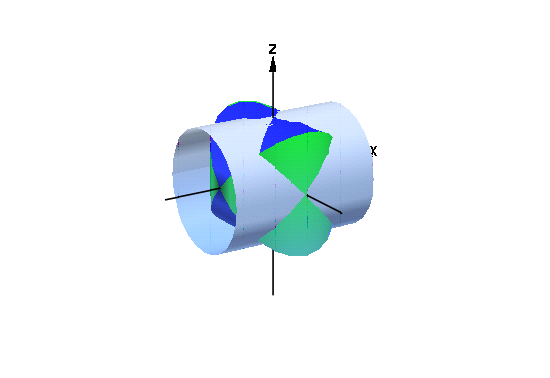
これで次のような曲面になります．

• plot(cone1,cone2,myAxes,Axes=None,Scaling=Constrained)

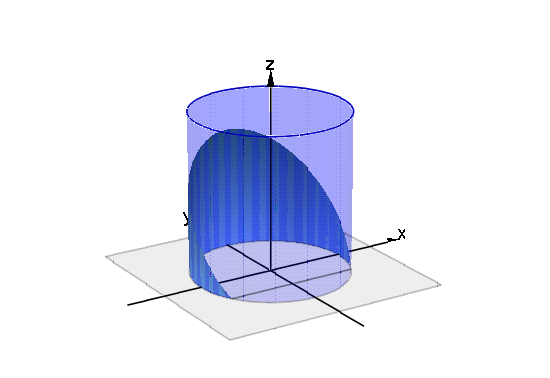
これに円柱も追加します．しかし，共通部分が見えるように，透過色にします．[0.2]は透過率が 0.2です．80%の光が通過します．

• twocones:=plot::Group3d(
  plot::Cone(1,[0,0,-2],1,[0,0,2],Color=RGB::Green.[0.2]),
  plot::Cone(1,[0,-2,0],1,[0,2,0],Color=RGB::Blue.[0.2]),
  plot::Circle3d(1,[0,0,-2],[0,0,1],FillColor=RGB::Green.[0.2],Filled=TRUE),
  plot::Circle3d(1,[0,0,2],[0,0,1],FillColor=RGB::Green.[0.2],Filled=TRUE),
  plot::Circle3d(1,[0,-2,0],[0,1,0],FillColor=RGB::Blue.[0.2],Filled=TRUE),
  plot::Circle3d(1,[0,2,0],[0,1,0],FillColor=RGB::Blue.[0.2],Filled=TRUE)
  ):
  

• plot(cone1,cone2,twocones,myAxes,Axes=None,Scaling=Constrained)
  

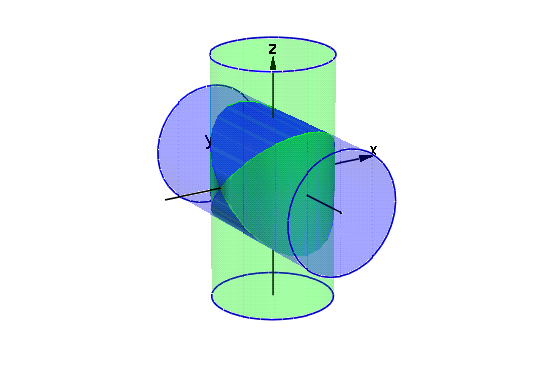
平面 z=k で切った断面をアニメーションで見てみます．

• cylinder1:=plot::Surface([sin(u),v,cos(u)],u=a..(2*PI-a),v=-3..3,a=0..PI):
  

• cylinder2:=plot::Surface([v,sin(u),cos(u)],u=a..(2*PI-a),v=-3..3,a=0..PI):
  

• crosssection:=plot::Group3d(
         Color=RGB::Grey40,
         plot::Surface([u,v,cos(a)],v=-sin(a)..sin(a),u=-3..-sin(a),a=0..PI),
                plot::Surface([-u,-v,cos(a)],v=-sin(a)..sin(a),u=-3..-sin(a),a=0..PI),
                plot::Surface([-u,-v,cos(a)],u=-sin(a)..sin(a),v=-3..-sin(a),a=0..PI),
                plot::Surface([u,v,cos(a)],u=-sin(a)..sin(a),v=-sin(a)..sin(a),a=0..PI),
         plot::Surface([u,v,cos(a)],u=-sin(a)..sin(a),v=-3..-sin(a),a=0..PI)):

• plot(cylinder1,cylinder2,crosssection,Color=RGB::Aqua,Scaling=Constrained)

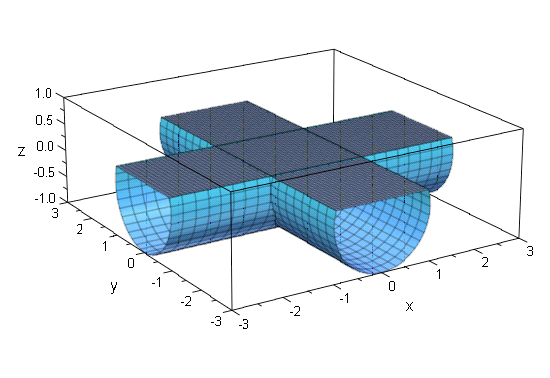
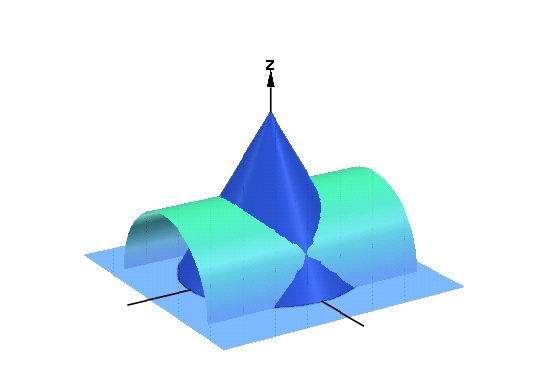
[2]. 3つの円柱 先の円柱に　「ｘ²＋ｙ²＝１」を付け加えます．Cone を使ってもできますが，Surface を使った方が良かったです．

• cone3:=plot::Surface([v,cos(u),sin(u)],u=0..2*PI,v=-1.3..1.3,
  ULinesVisible=FALSE,VLinesVisible=FALSE,Color=RGB::Grey)
  

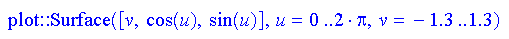
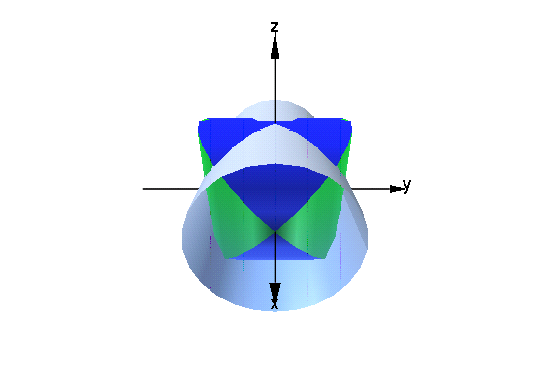
これで次のようになります．

• plot(cone1,cone2,cone3,myAxes,Axes=None,Scaling=Constrained)
  

さらに camera object　を使うと，アニメーションにもなります．

• mycamera := plot::Camera([3.5*cos(a), 4*sin(a), 1 + cos(2*a)],
                         [0, 0, 0], 1.1*PI/3, a = 0..2*PI,
                         Frames = 100):

• plot(cone1,cone2,cone3,mycamera,myAxes,Axes=None,Scaling=Constrained)
  

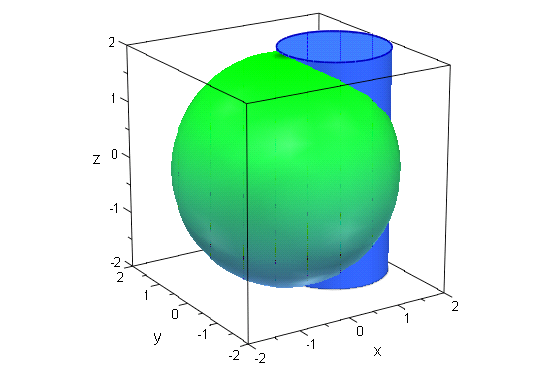
[3]. 球と円柱， 「原点中心で半径が2の球」と 「軸がx=1,y=0で半径が1の円柱」.　球は plot::Sphere (low level primitive)を使っても描けますが，交線は plot::Surface や plot::Spherical （ともに high level primitive) の方がきれいになります．

•  cylinder1:=plot::Group3d(
          plot::Cone(1,[1,0,-2],1,[1,0,2]),
          plot::Circle3d(1,[1,0,2],Filled=TRUE)
     ):   
  

• sphere:=plot::Spherical([2,u,v],u=0..2*PI,v=0..PI,
  Color=RGB::Green,ULinesVisible=FALSE,VLinesVisible=FALSE):
      
  

• plot(cylinder1,sphere)

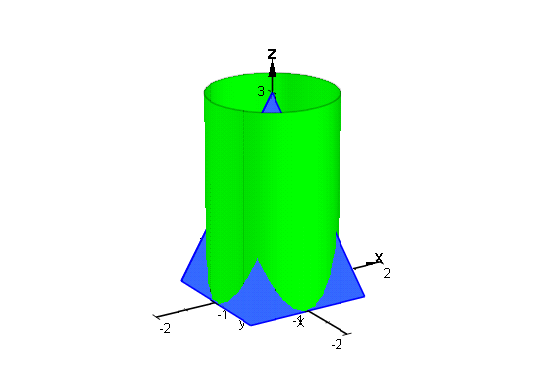
[4]. 円柱と三角錐 三角錐を Polygon3d を4つ組み合わせて作ります．Polygon3d は 点を無数につなげられますが,中を塗りつぶせるのは三角形のときだけです．

• pyramid:=plot::Group3d(
       plot::Polygon3d([[1,-1,0],[1,1,0],[0,0,3]],Filled=TRUE),  
       plot::Polygon3d([[1,1,0],[-1,1,0],[0,0,3]],Filled=TRUE),  
       plot::Polygon3d([[-1,-1,0],[-1,1,0],[0,0,3]],Filled=TRUE),
       plot::Polygon3d([[-1,-1,0],[1,-1,0],[0,0,3]],Filled=TRUE)):
  
      
  
  

• cylinder2:=plot::Cone(1,[0,0,0],1,[0,0,3],Color=RGB::Green):
      
  
  

• myAxes2:=plot::Group3d(
  plot::Arrow3d([-2,0,0],[2,0,0],Color=RGB::Black),plot::Text3d("x",[2,0,0])
  ,plot::Arrow3d([0,-2,0],[0,2,0],Color=RGB::Black),plot::Text3d("y",[0,2,0])
  ,plot::Arrow3d([0,0,0],[0,0,3.5],Color=RGB::Black),plot::Text3d("z",[0,0,3.5])):

• plot(cylinder2,pyramid,Scaling=Constrained,myAxes2,Axes=Origin)
  

[5].円柱と平面 　円柱 「x²+y²=1」 と　平面 「z=y+1/2」を描いてみます．まず　xy平面と円柱を作ります．円柱の色は透過率を 0.2 にします．

• xyplane:=plot::Parallelogram3d([0,0,0],[1.5,0,0],[0,1.5,0],Color=RGB::Grey):

• cone4:=plot::Group3d(
            plot::Cone(1,[0,0,0],1,[0,0,2],Color=RGB::Blue.[0.2]),
            plot::Circle3d(1,[0,0,2],FillColor=RGB::Blue.[0.2],Filled=TRUE)):
  

切り口の平面は 「(x,y,z)=(u, sin(t), sin(t)+1/2), u=-cos(t)..cos(t), t=-pi/6..pi/2 」ですが，MuPADでは変域が定数でないといけないので，次のように作ります．

• plane:=plot::Surface([s*cos(t),sin(t),sin(t)+1/2],s=-1..1,t=-PI/6..PI/2,Color=RGB::DarkGreen):
  

同様に円すいの側面のうち 0<z<y+1/2 に挟まれる領域は 「(x,y,z)=(cos(t),sin(t),v) t=-pi/6..7pi/6 ,v=0..sin(t)+1/2」ですから，次のように作ります.

• side:=plot::Surface([cos(t),sin(t),s*(sin(t)+1/2)],s=0..1,t=-PI/6..7/6*PI,Color=RGB::DarkGreen):

• myAxes2:=plot::Group3d(
  plot::Arrow3d([-2,0,0],[2,0,0],Color=RGB::Black),plot::Text3d("x",[2,0,0])
  ,plot::Arrow3d([0,-2,0],[0,2,0],Color=RGB::Black),plot::Text3d("y",[0,2,0])
  ,plot::Arrow3d([0,0,0],[0,0,2.5],Color=RGB::Black), plot::Text3d("z",[0,0,2.5])):

• plot(plane,side,cone4,xyplane,myAxes2,Axes=None,ULinesVisible=FALSE,VLinesVisible=FALSE)
  

さらに平面 「y=k」を付け加えてアニメーションにして見ます.

• movingplane:=plot::Parallelogram3d(
         [0,sin(t),(sin(t)+0.5)/2],[cos(t),0,0],[0,0,(sin(t)+0.5)/2],t=-PI/6..PI/2):

• plot(side,cone4,xyplane,movingplane,myAxes2,Axes=None,ULinesVisible=FALSE,VLinesVisible=FALSE)

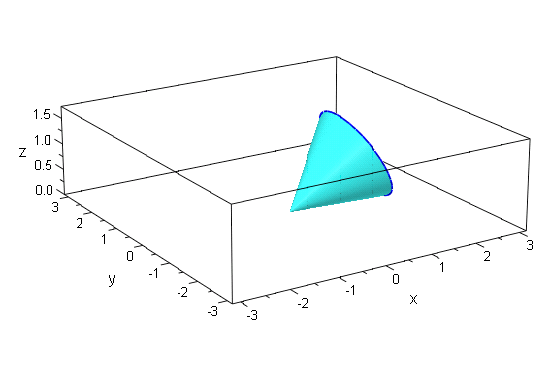
[6]. 円すいと円柱「頂点が(0,0,2)で底面の半径が 2/√3 の円の円すい」と 「軸がx軸上にあり半径が１の円柱」，この二つは yz 平面で接します．

• XYplane:=plot::Surface([u,v,0],u=-1.7..1.7,v=-1.7..1.7,ULinesVisible=FALSE,
  VLinesVisible=FALSE):

• cone5:=plot::Surface([v,cos(u),sin(u)],u=0..PI,v=-1.5..1.5,
  ULinesVisible=FALSE,VLinesVisible=FALSE,Color=RGB::Green):

• cone6:=plot::Cone(2/sqrt(3),[0,0,0],0,[0,0,2]):

• plot(cone5,cone6,XYplane,myAxes2,Axes=None)
  

[7]. xy平面上を回転しながら回る円すい．
Rotate3d(theta, object) で z軸の周りのtheta の回転になりますが，これに theta=0..2pi　を付け加えることで　簡単にアニメーションになります．

• conebasic:=plot::Group3d(
       plot::Cone(1,[3/2,0,sqrt(3)/2],[0,0,0],FillColor=RGB::Aqua),
       plot::Circle3d(1,[3/2,0,sqrt(3)/2],[3/2,0,sqrt(3)/2],Filled=TRUE)
       ):
  

• rotatingcone:=plot::Rotate3d(theta,conebasic,theta=0..2*PI):

• plot(rotatingcone)

z=k(k=1)を付け加えて断面を見ます

• plane1:=plot::Parallelogram3d([0,0,1],[3,0,0],[0,3,0],Color=RGB::Green)

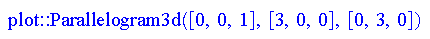
• plot(plane1,rotatingcone,myAxes2)