[1]. 区分求積法
区間は[0,1], 関数はf で , ∑k=1n f(k/n) のタイプ
少し長くなるので proc を使ってプログラミングします.
piecewise([condition,object]) と
数列生成子「$」を組み合わせることにより n個の条件とn個の階段を一度に作りました.これを
plot::Function2d に変換し stepfunc を作りました.このままでも
plot できますが「階段の枠」が見えるだけなので,それを
plot::Hatch を使って塗りつぶしました.
(なお plot::Hatch は plot::Function2d か plot::Curve2d
でないと受け付けません.)
- myStepfunc:=proc(n,f)
local myfunc,peaks,stepfunc,walls,rightwall,bottomwall;
begin
myfunc:=f:
peaks:=x->piecewise([k/n<=x and x<(k+1)/n, f((k+1)/n)] $k=0..n-1):
stepfunc:=plot::Function2d(peaks(x),x=0..1,Color=RGB::Black):
walls:=plot::Curve2d([t/n,y],y=0..max(f((t)/n),f((t+1)/n)),Color=RGB::Black)$t=0..n-1:
rightwall:=plot::Curve2d([1,y],y=0..f(1),Color=RGB::Black):
bottomwall:=plot::Function2d(0,x=0..1,Color=RGB::Black):
plot(stepfunc(x),plot::Hatch(stepfunc(x),FillPattern=Solid,FillColor=RGB::ForestGreen),
walls,rightwall,bottomwall,plot::Function2d(f(x),x=0..1),Header="n=".expr2text(n))
end_proc
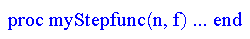
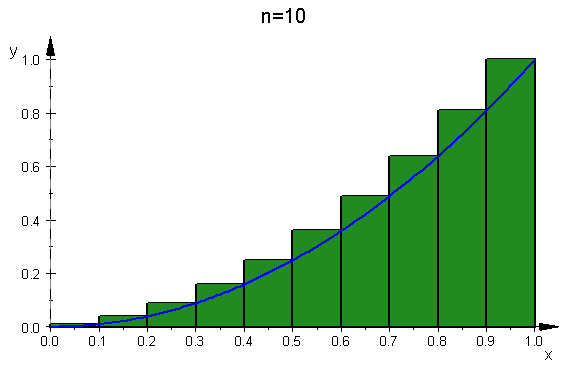
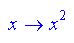 f(x)=x2 で n=10, n=50 の時です.
f(x)=x2 で n=10, n=50 の時です.
- myStepfunc(10,f);myStepfunc(50,f)

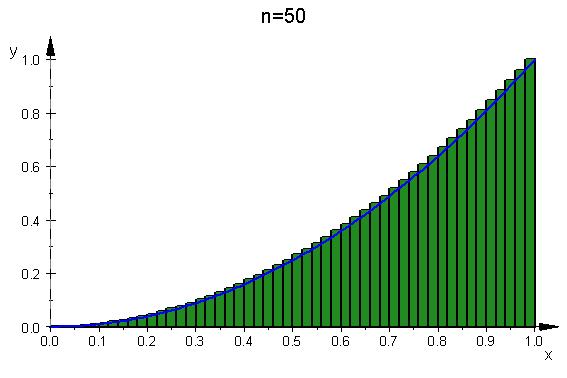

次は n による変化が良く分かるようにアニメーションにします.そのために 返り値を plot object にして,その plot object の TimeRange 変数に渡すために
新しく time という引数を付け加えます.この引数は plot(plot object) のとき VisibleBeforeBegin=FALSE, VisibleAfterEnd=FALSE と一緒に使われて
指定された時間だけアニメーションを表示させます.例えば 「time=0..5」 とすると 「TimeRange=0..5」 となり 0から5秒の間しか表示されません.
なお,Header はアニメーションにできないのでplot::Text2d に変更します.
(MuPADでは 殆ど全てのobjectはアニメーションになりますが,これは数少ない例外のひとつです.)
- stepAnimation:=proc(n,f,time)
local myfunc,peaks,stepfunc,stepfuncs,walls,rightwall,bottomwall;
begin
myfunc:=f:
peaks:=x->piecewise([k/n<=x and x<(k+1)/n, f((k+1)/n)] $k=0..n-1):
stepfunc:=plot::Function2d(peaks(x),x=0..1,Color=RGB::Black):
walls:=plot::Curve2d([t/n,y],y=0..max(f((t)/n),f((t+1)/n)),Color=RGB::Black)$t=0..n-1:
rightwall:=plot::Curve2d([1,y],y=0..f(1),Color=RGB::Black):
bottomwall:=plot::Function2d(0,x=0..1,Color=RGB::Black):
myheader:=plot::Text2d("n=".expr2text(n),[0.5,1],TextFont=[15]):
stepfuncs:=plot::Group2d(stepfunc(x),plot::Hatch(stepfunc(x),FillPattern=Solid,
FillColor=RGB::ForestGreen),walls,rightwall,bottomwall,
plot::Function2d(f(x),x=0..1),myheader,
TimeRange=time);
return(stepfuncs):
end_proc
time=0..10 にしていますが,VisibleBeforeBegin,VisibleAfterEnd を指定してないので,無関係です.返り値が plot object なので
「plot( )」 の形で使います.
- plot(stepAnimation(10,f,0..10))
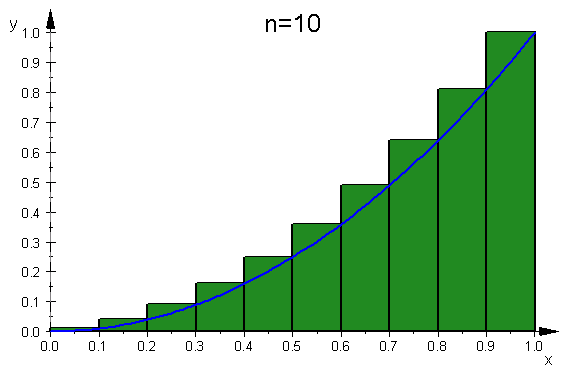

数列生成子「$」を使って,stepAnimation(5,f,2..4),stepAnimation(10,f,4..6)...のような 列を作って一度にアニメーションさせます.今度は
VisibleBeforeBegin,VisibleAfterEnd の値を FALSE にしているので,与えられた TimeRange の間しか表示されません.
- plot(stepAnimation(5*k,f,2*k..2*(k+1))$k=1..10,VisibleBeforeBegin=FALSE,VisibleAfterEnd=FALSE)
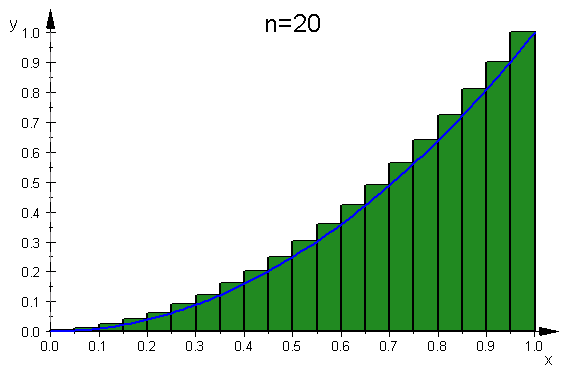

[2]. 置換積分と微小面積 (その1)
f(x)=2x ex2の区間[0,1]における積分をI,
g(t)=et の区間[0,1] における積分をJとして
「ΔI=2xΔx,ΔJ=etΔt が微小面積として等しいこと 」 を示すCGをかきます.
(ただし t=x2)
まず ΔIやΔJが「正の時は微小面積を緑色」で,「負の時は青色」で表したいので myColor を定義します.
- myColor:=x->piecewise([x<0,RGB::Blue],[x>=0,RGB::ForestGreen]):
f(g(x))g'(x), t=g(x), f(t) を「手動で」定義します.(f(g(x)g'(x))は合成関数なので「自動で」表すこともできます)
- f:=x->exp(x^2)*2*x: g:=x->x^2: h:=t->exp(t):
分割数 n を10にして xの区間[0,1]を n 等分し 「xの」分割の幅 Δx を 定義します.
「塗りつぶし」は plot::Hatch を使いますが , plot::Hatch は plot::Function2d または plot::Curve2d しか受け付けません.
- sceneA:=plot::Hatch(plot::Function2d(f,x=k*delta..(k+1)*delta),TimeRange=k..k+1,
FillPattern=Solid,FillColor=myColor(f(k*delta)))$k=0..n-1:
sceneB:=plot::Hatch(plot::Function2d(h,t=g(k*delta)..g((k+1)*delta)),TimeRange=k..k+1,
FillPattern=Solid,FillColor=myColor(h(g(k*delta))*g'(k*delta)))$k=0..n-1:
1つのCanvasに入れるために plot::Scene を使って,Scene object を2つ作ります.このとき,2つの シーンの縮尺を同じにするために「手動で」
Scene のサイズを変更します.( Width,Height はそれぞれ「幅」と「高さ」を表しますが,TopMargin,BottomMargin も指定しないとうまく行かないようです.)
- figA:=plot::Scene2d(sceneA,plot::Function2d(f,x=0..1,TimeRange=0..n,Color=RGB::Black),
Header="2x*e^(x^2)",Width=40*unit::mm):
figB:=plot::Scene2d(sceneB,plot::Function2d(h,t=0..1,TimeRange=0..n,Color=RGB::Black),
Header="e^t",XAxisTitle="t",Height=120*unit::mm,
TopMargin=17*unit::mm,BottomMargin=16*unit::mm):
「Scene objects」 を「plot」すると,1つのCanvasに表示されます.
- plot(figA,figB,VisibleBeforeBegin=FALSE,VisibleAfterEnd=FALSE,BorderWidth = 0.5*unit::mm );
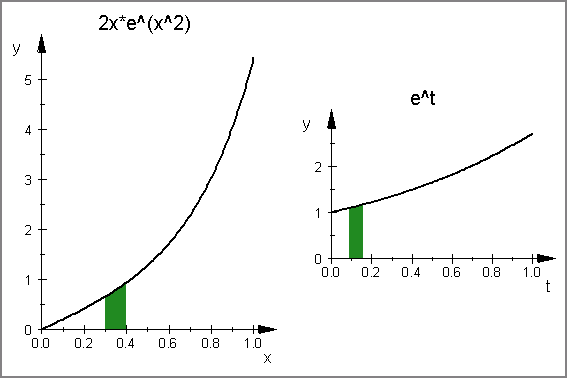

以上の手続きはプログラムすることもできます.しかし,Scene のサイズは(私の知る限りでは)「手動で」手直ししないといけないので,全てをプログラミングすることはできません.
[3]. 置換積分と微小面積
(その2) f(x)=(x2-1) ex3-3x の区間[0,√3]における積分をI,
g(t)=et/3 の区間[0, 0] における積分をJとして
「ΔI=(x2-1) ex3-3x) Δx, ΔJ=et/3 Δt が微小面積として等しいこと」
を示すCGをかきます.
(ただし t=x3-3x)
先の例と殆ど同じですが
「x が増加しても
t が減少することがある」ので,sceneB
で 変域の指定に
max, min を使っています.
- myColor:=x->piecewise([x<0,RGB::Blue],[x>=0,RGB::ForestGreen]):
- f:=x->exp(x^3-3*x)*(x^2-1): g:=x->x^3-3*x: h:=t->exp(t)/3:
n:=20: delta:=(sqrt(3)-0)/n:
- sceneA:=plot::Hatch(plot::Function2d(f,x=k*delta..(k+1)*delta),TimeRange=k..k+1,
FillPattern=Solid,FillColor=myColor(f(k*delta)))$k=0..n-1:
sceneB:=plot::Hatch( plot::Function2d(h,t=min(g(k*delta),g((k+1)*delta))..
max(g(k*delta),g((k+1)*delta))),TimeRange=k..k+1,
FillPattern=Solid,
FillColor=myColor(h(g(k*delta))*g'(k*delta))
)$k=0..n-1:
- figA:=plot::Scene2d(sceneA,plot::Function2d(f,x=0..sqrt(3),TimeRange=0..n,Color=RGB::Black),
Header="(x^2-1)*e^(x^3-3x)",Height=180*unit::mm):
figB:=plot::Scene2d(sceneB,plot::Function2d(h,t=-2..0,TimeRange=0..n,Color=RGB::Black),
Header="e^t/3",XAxisTitle="t",Height=120*unit::mm,
TopMargin=26*unit::mm,BottomMargin=26*unit::mm):
- plot(figA,figB,VisibleBeforeBegin=FALSE,VisibleAfterEnd=FALSE,BorderWidth = 0.5*unit::mm);
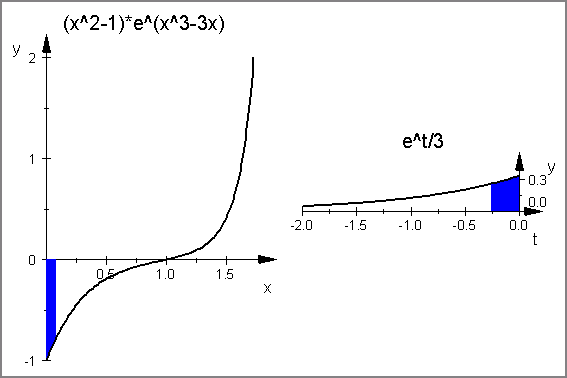

[4]. cycloid の軌跡
サイクロイド: (x,y)=(t-sin(t),1-cos(t)) の軌跡のアニメーション.
- mycycloid:=plot::Curve2d([u-sin(u),1-cos(u)],u=0..t,t=0..2*PI,
Color=RGB::Black,LineStyle=Dashed):
- mypoint:=plot::Point2d([t-sin(t),1-cos(t)],t=0..2*PI,Color=RGB::Black,PointSize=2):
- mycircle:=plot::Circle2d(1,[t,1],t=0..2*PI,Color=RGB::Blue):
- plot(mycircle,mypoint,mycycloid)
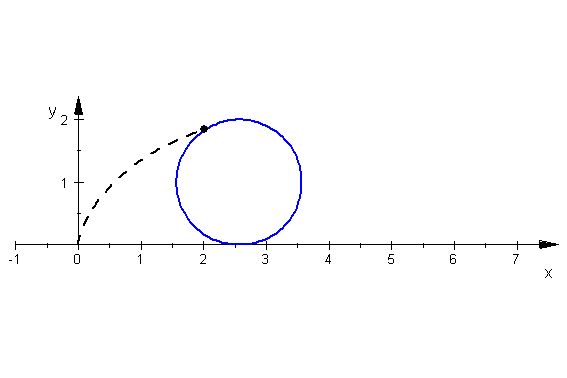

[5]. 面積と置換積分(その1)-cycloid と x 軸で囲まれる領域の面積と置換積分
(x,y)=(t-sin(t),1-cos(t)) において,
微小面積 yΔx=(1-cos(t))2 Δt.
「yΔx」と 「(1-cos(t))2 Δt 」 を比べて等しいことを見ます.
- X:=t->t-sin(t):Y:=t->1-cos(t):
nはtの分割数です.X(t),Y(t)はサイクロイドの式です.
微小細片の塗りつぶしは plot::Hatch(plot::Curve2d) を使います.しかし,cycloid の式は陽関数に直せないので,
P(X(t),0), Q(X(t),Y(t)), R(X(t+delta),Y(t+delta)), S(X(t+delta),0) を通る閉曲線を plot::Curve を使って作ります.
- Fx:=(t,s,X,delta)->piecewise([0<=s and s<=1,X(t)],[1<s and s<2,X(t+delta*(s-1))],
[2<=s and s<=3,X(t+delta)],[3<s and s<=4,(s-3)*X(t)+(4-s)*X(t+delta)]):
- Fy:=(t,s,Y,delta)->piecewise([0<=s and s<=1,Y(t)*s],[1<s and s<2,Y(t+delta*(s-1))],
[2<=s and s<=3,Y(t+delta)*(3-s)],[3<s and s<=4,0]):
(Fx(t,s),Fy(t,s))は「0<s<1のとき 線分PQ」, 「1<s<2のとき 線分QR」,「2<s<3のとき 線分RS」,「3<s<4のとき 線分SP」を描きます.
下で 「s=0..3」にしているのは plot::Hatch(「plot::Curve2d object」)は自動的に閉曲線を作るからです.
このCycを使って plot::Scene object の scene1 を作ります.
- Cyc:=plot::Hatch(plot::Curve2d([Fx(delta*t,s,X,delta),Fy(delta*t,s,Y,delta)],s=0..3),
FillPattern=Solid,TimeRange=t..t+1,FillColor=RGB::ForestGreen
)$t=0..n-1:
scene1:=plot::Scene2d(Cyc,plot::Curve2d([u-sin(u),1-cos(u)],u=0..2*PI,
Color=RGB::Black,TimeRange=0..n),Height=80*unit::mm,Footer="Cycloid"):
(1-cos(t))2 Δt に関しても塗りつぶしを作りますが,こちらは陽関数なので
plot::Function2d に直して
plot::Hatch を使います.
- Cyc2:=plot::Hatch(plot::Function2d((1-cos(th))^2,th=delta*t..delta*(t+1)),
FillPattern=Solid,TimeRange=t..t+1,FillColor=RGB::ForestGreen)$t=0..n-1:
scene2:=plot::Scene2d(Cyc2,plot::Function2d((1-cos(th))^2,th=0..2*PI,Color=RGB::Black,TimeRange=0..n),
XAxisTitle="t",Height=80*unit::mm,Footer="(1-cos t)^2"):
- plot(plot::Canvas(scene1,scene2,VisibleBeforeBegin=FALSE,VisibleAfterEnd=FALSE,
Scaling=Constrained,Width = 120*unit::mm,
Height = 80*unit::mm,BorderWidth = 0.5*unit::mm ))
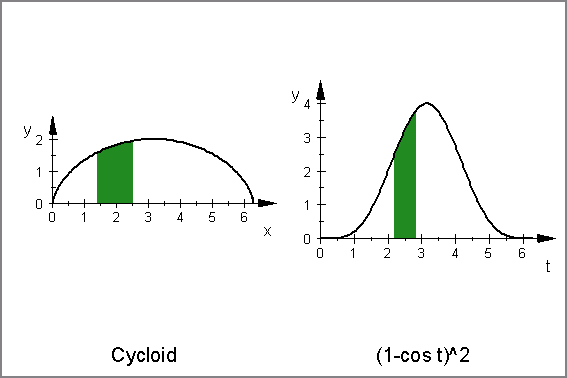

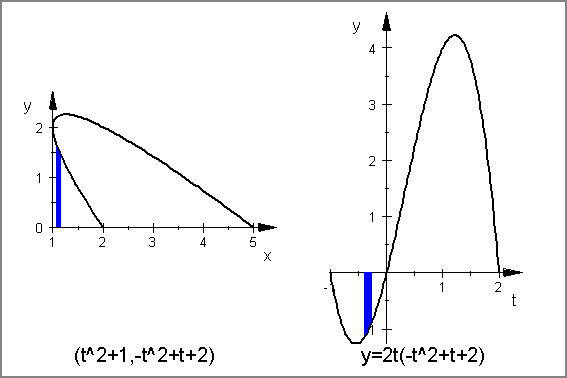
[6]. 面積と置換積分(その2)- (x,y)=(t2+1, -t2+t+2) と x軸で囲まれる面積と置換積分
(x,y)=(t2+1,-t2+t+2) において, 微小面積 yΔx=(-t2+t+2)*(2tΔt).
「yΔx」 と 「2t(-t2+t+2) Δt 」を比べて等しいことを見ます.このとき
「yΔx」や 「2t(-t2+t+2) Δt 」
が「正のときは緑色」で,「負の時は青色で」表します.それ以外は殆ど同じです.
- myColor:=x->piecewise([x<=0,RGB::Blue],[x>0,RGB::ForestGreen]):
- X:=t->t^2+1: Y:=t->-t^2+t+2:
- n:=20: delta:=(2-(-1))/n:
tの区間 「-1<t<2」 を n(=20) 個に分割しました.先の例で使ったFx(t,s),Fy(t,s)を使って
P(X(t),0), Q(X(t),Y(t)), R(X(t+delta),Y(t+delta)), S(X(t+delta),0) を通る閉曲線を plot::Curve を使って作ります.
この閉曲線PQRSを plot::Hatchを使って塗りつぶし,plot::Scene2d に埋め込みます.
- c:=plot::Hatch(plot::Curve2d([Fx(delta*t-1,s,X,delta),Fy(delta*t-1,s,Y,delta)],s=0..3),
FillPattern=Solid,FillColor=myColor(X'(delta*t-1)),TimeRange=t..t+1)$t=0..n-1:
//tの変域が -1 からなので Fx,Fyの式で 「delta*t-1」 になる
- scene3:=plot::Scene2d(c,plot::Curve2d([u^2+1,-u^2+u+2],u=-1..2,
Footer="(t^2+1,-t^2+t+2)",
Color=RGB::Black,TimeRange=0..n),Height=60*unit::mm,Width=100*unit::mm):
「2t(-t2+t+2) Δt」の方は陽関数なので
plot::Hatch(plot::Function2d object)で作り,plot::Scene2d
に埋め込みます.
- d:=plot::Hatch(plot::Function2d(Y(th)*diff(X(th),th),th=delta*t-1..delta*(t+1)-1),
FillPattern=Solid,Color=myColor(Y(delta*t-1)*X'(delta*t-1)),TimeRange=t..t+1)$t=0..n-1:
scene4:=plot::Scene2d(d,plot::Curve2d([u,Y(u)*diff(X(u),u)],u=-1..2,
Color=RGB::Black,TimeRange=0..n),Footer="y=2t(-t^2+t+2)",
XAxisTitle="t",
Height=60*unit::mm,Width=25*unit::mm
):
- plot(scene3,scene4,VisibleBeforeBegin=FALSE,VisibleAfterEnd=FALSE,
Scaling=Constrained,BorderWidth = 0.5*unit::mm)

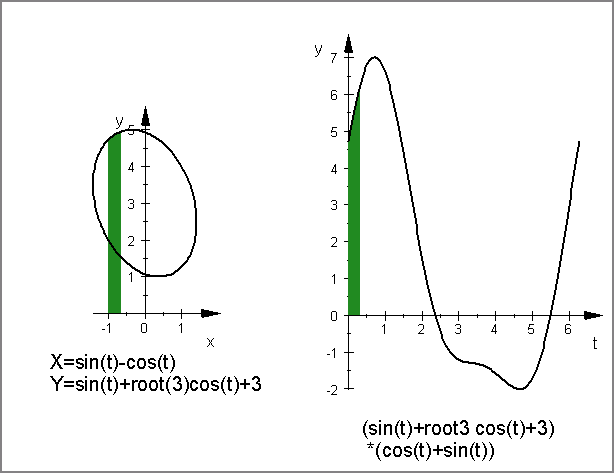
[7]. 面積と置換積分(その3)- C:(x,y)=(sin(t)-cos(t),
sin(t)+√3cos(t)+3) で囲まれる面積と置換積分
(x,y)=(sin(t)-cos(t), sin(t)+√3cos(t)+3)
において, 微小面積 yΔx=(sin(t)+√3cos(t)+3)*(cos(t)+sin(t))Δt.
「yΔx」 と 「(sin(t)+√3cos(t)+3)*(cos(t)+sin(t))Δt
」を比べて等しいことを見ます.先の例と殆ど同じです.
myColor に, x の大小が判定しずらい場合にも対応するように
float を入れます.
- myColor:=x->piecewise([float(x)<0,RGB::Blue],[float(x)>=0,RGB::ForestGreen]):
- X:=t->sin(t)-cos(t): Y:=t->sin(t)+sqrt(3)*cos(t)+3:
tの区間 「0<t<2pi」 を n(=20) 個に分割しました.2つ前の例で使ったFx(t,s),Fy(t,s)を使って
P(X(t),0), Q(X(t),Y(t)), R(X(t+delta),Y(t+delta)), S(X(t+delta),0) を通る閉曲線を plot::Curve を使って作ります.
この閉曲線PQRSを plot::Hatchを使って塗りつぶし,plot::Scene2d に埋め込みます.
- c:=plot::Hatch(plot::Curve2d([Fx(delta*t,s,X,delta),Fy(delta*t,s,Y,delta)],s=0..3),
FillPattern=Solid,FillColor=myColor(X'(delta*t)),TimeRange=t..t+1)$t=0..n-1:
- scene5:=plot::Scene2d(c,plot::Curve2d([X(u),Y(u)],u=0..2*PI,
Color=RGB::Black,TimeRange=0..n),
Footer="X=sin(t)-cos(t)\nY=sin(t)+root(3)cos(t)+3",
TopMargin=21*unit::mm,BottomMargin=15*unit::mm):
- d:=plot::Hatch(plot::Function2d(Y(th)*diff(X(th),th),th=delta*t..delta*(t+1)),
FillPattern=Solid,Color=myColor((Y(t*delta)*X'(t*delta))),TimeRange=t..t+1)$t=0..n-1:
scene6:=plot::Scene2d(d,plot::Curve2d([u,Y(u)*diff(X(u),u)],u=0..2*PI,
Color=RGB::Black,TimeRange=0..20),
Footer="(sin(t)+root3 cos(t)+3)\n *(cos(t)+sin(t))",
XAxisTitle="t"):
- plot(scene5,scene6,VisibleBeforeBegin=FALSE,VisibleAfterEnd=FALSE,
Scaling=Constrained,Height=100*unit::mm,Width=130*unit::mm,
BorderWidth = 0.5*unit::mm)

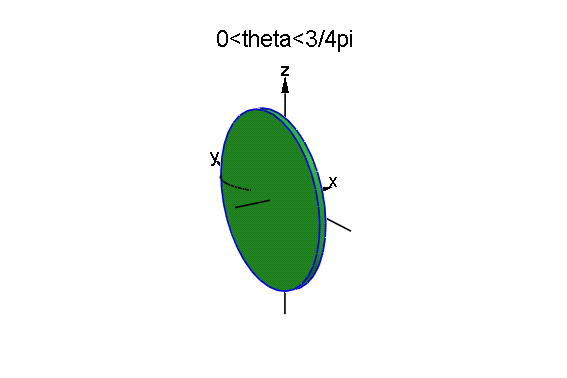
[8] パラメーター表示曲線の回転体
(x,y)=(sin(t)-cos(t), sin(t)+√3cos(t)) で表される曲線を
x軸の周りに回転した立体の体積を細分してみる.
微小円盤の体積 ΔV=π y2 Δx=π (sin(t)+√3cos(t)+3)^2*(cos(t)+sin(t))Δt.
「π y2 Δx」 と 「π (sin(t)+√3cos(t)+3)2*(cos(t)+sin(t))Δt 」を比べて等しいことを見ます.
「MuPADのプログラムのエラーで X'(t)=0のときに不要な楕円が描かれる」ので,それに対応するために epsilon
をつけた.(^_^;)
- epsilon:=0.001:
X:=t->sin(t+epsilon)-cos(t+epsilon):
Y:=t->sin(t+epsilon)+sqrt(3)*cos(t+epsilon)+3:
disk1は t=0..3/4π , disks2は t=3/4π..7/4π ,disks3は
t=7/4π..2πにおける「円盤」の集まり.
- disks1:=plot::Group3d(plot::Circle3d(Y(t*delta),[X(t*delta),0,0],[1,0,0]),
plot::Circle3d(Y(t*delta),[X((t+1)*delta),0,0],[1,0,0]),
Color=myColor(X'(t*delta)),Filled=TRUE,TimeRange=t..8)$t=0..7:
disks2:=plot::Group3d(plot::Circle3d(Y(t*delta),[X(t*delta),0,0],[1,0,0]),
plot::Circle3d(Y(t*delta),[X((t+1)*delta),0,0],[1,0,0]),
Color=myColor(X'(t*delta)),TimeRange=t..18,FillColor=RGB::Aqua,Filled=TRUE)$t=8..17:
disks3:=plot::Group3d(plot::Circle3d(Y(t*delta),[X(t*delta),0,0],[1,0,0]),
plot::Circle3d(Y(t*delta),[X((t+1)*delta),0,0],[1,0,0]),
Color=myColor(X'(t*delta)),TimeRange=t..20,Filled=TRUE)$t=18..20:
cones1は t=0..3/4π , cones2は t=3/4π..7/4π ,cones3は
t=7/4π..2πにおける円柱の「側面」の集まり.
- cones1:=plot::Cone(Y(t*delta),[X(t*delta),0,0],Y(t*delta),[X((t+1)*delta),0,0],
Color=myColor(X'(t*delta)),TimeRange=t..8)$t=0..7:
cones2:=plot::Cone(Y(t*delta),[X(t*delta),0,0],Y(t*delta),[X((t+1)*delta),0,0],
Color=myColor(X'(t*delta)),TimeRange=t..18)$t=8..17:
cones3:=plot::Cone(Y(t*delta),[X(t*delta),0,0],Y(t*delta),[X((t+1)*delta),0,0],
Color=myColor(X'(t*delta)),TimeRange=t..20)$t=18..20:
- texts:=plot::Group3d(
plot::Text3d("0<theta<3/4pi",[0,0,8],TextFont=[14],TimeRange=0..8),
plot::Text3d("3/4pi<theta<7/4pi",[0,0,8],TextFont=[14],TimeRange=8..18),
plot::Text3d("7/4pi<theta<2pi",[0,0,8],TextFont=[14],TimeRange=18..20)
):
- myAxes:=plot::Group3d(
plot::Arrow3d([-3,0,0],[3,0,0],Color=RGB::Black),plot::Text3d("x",[3,0,0])
,plot::Arrow3d([0,-6,0],[0,7,0],Color=RGB::Black),plot::Text3d("y",[0,7,0])
,plot::Arrow3d([0,0,-6.5],[0,0,6.5],Color=RGB::Black),plot::Text3d("z",[0,0,6.5])
):
c:=plot::Curve3d([sin(t)-cos(t),sin(t)+sqrt(3)*cos(t)+3,0],t=0..2*PI,Color=RGB::Black):
- plot(cones1,cones2,cones3,disks1,disks2,disks3,texts,TimeRange=0..20,
VisibleBeforeBegin=FALSE,VisibleAfterEnd=FALSE,c,myAxes,Axes=None)

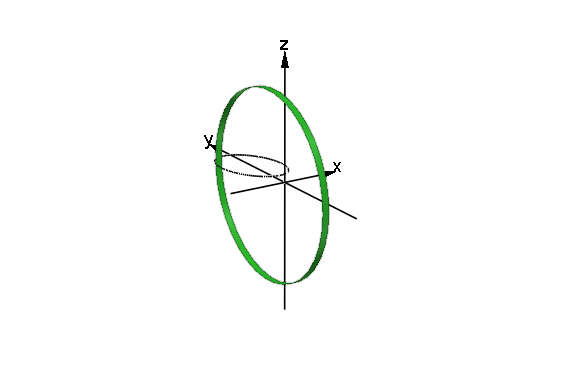
円柱の側面だけを plot すると次のようになる.
- plot(cones1,cones2,cones3,TimeRange=0..20,
VisibleBeforeBegin=FALSE,c,myAxes,Axes=None)

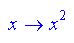 f(x)=x2 で n=10, n=50 の時です.
f(x)=x2 で n=10, n=50 の時です.